Уравнение
(31.11), играющее в относительном движении ту же роль, что и закон Ньютона
(31.4) – в абсолютном движении, и выражает собою основной закон динамики
относительного движения. Из сравнения (31.4) и (31.11) заключаем, что уравнение
относительного движения точки (в неинерциальной системе ![]() )
можно составлять так же, как уравнения абсолютного движения (в инерциальной
системе
)
можно составлять так же, как уравнения абсолютного движения (в инерциальной
системе ![]() ), если к действительным силам прибавить
переносную и кориолисову силы инерции.
), если к действительным силам прибавить
переносную и кориолисову силы инерции.
Таким образом,
силы инерции ![]() ,
, ![]() представляют
собою поправки на неинерциальность системы отсчета. Эти векторы были названы
силами, благодаря силовой размерности этих величин и возможности измерять их
действие динамометром. Однако их еще нельзя отождествлять с действительными
силами. Последнее невозможно по той причине, что действительные силы – всегда
силы взаимодействия материальных тел, силы же инерции относительного движения
этим свойством не обладают ввиду отсутствия материального источника, так как
нельзя указать материальные тела, порождающие эти силы.
представляют
собою поправки на неинерциальность системы отсчета. Эти векторы были названы
силами, благодаря силовой размерности этих величин и возможности измерять их
действие динамометром. Однако их еще нельзя отождествлять с действительными
силами. Последнее невозможно по той причине, что действительные силы – всегда
силы взаимодействия материальных тел, силы же инерции относительного движения
этим свойством не обладают ввиду отсутствия материального источника, так как
нельзя указать материальные тела, порождающие эти силы.
2°. Начальная задача.
Представив
векторы ![]() и
и ![]() (входящие
в уравнение относительного движения (31.11)) в базисе
(входящие
в уравнение относительного движения (31.11)) в базисе ![]() подвижной
системы и приравняв соответствующие компоненты равных векторов, получим систему
трех уравнений
подвижной
системы и приравняв соответствующие компоненты равных векторов, получим систему
трех уравнений
![]()
![]() ,
(31.13)
,
(31.13)
![]() ,
, ![]() ,
,
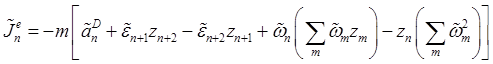 (инд.
(инд.![]() ), которые называют
дифференциальными уравнениями относительного движения в декартовых координатах.
Присоединив к уравнениям начальные условия:
), которые называют
дифференциальными уравнениями относительного движения в декартовых координатах.
Присоединив к уравнениям начальные условия:
![]() ,
, ![]() ,
, ![]()
![]() ,
(31.15)
,
(31.15)
получим начальную задачу для относительного движения. При обычных условиях на силы (включая силы инерции) эта задача имеет единственное решение.
3°. Принцип относительности Галилея.
Рассмотрим
частный случай относительного движения, в котором среда ![]() (и
связанная с ней подвижная система
(и
связанная с ней подвижная система ![]() ) движется
поступательно, равномерно и прямолинейно, т.е. среда не вращается, а полюс
) движется
поступательно, равномерно и прямолинейно, т.е. среда не вращается, а полюс ![]() движется равномерно и прямолинейно:
движется равномерно и прямолинейно:
![]() ,
, ![]()
![]() .
.
Тогда ускорение полюса, а также угловая скорость и угловое ускорение среды равны нулю.
![]() ,
, ![]() ,
, ![]() .
.
При этом переносная и кориолисова силы инерции обращаются в нуль
![]() ,
, ![]()
и основное уравнение динамики относительного движения (31.11) принимает такой же вид, как и динамическое уравнение абсолютного движения:
![]() .
(31.16)
.
(31.16)
Это означает, что относительное движение тела будет происходить по тем же законам, что и абсолютное; следовательно, подвижная система отсчета также будет инерциальной. Таким образом, инерциальных систем отсчета оказывается бесчисленное множество; в силу предыдущего всякая система, движущаяся поступательно, равномерно и прямолинейно относительно инерциальной системы, также будет инерциальной системой.
Во всех инерциальных системах отсчета динамические уравнения движения имеют одинаковый вид, и, значит, все эти системы равноправно, ибо нет никаких физических оснований предпочесть одну из этих систем другой. Вопрос о том, какая из двух инерциальных систем отсчета покоится, а какая движется, оказывается лишенным физического смысла.
Равноправность всех инерциальных систем является объективной реальностью. Утверждение этой равноправности называют принципом относительности Галилея.
4°. Относительное равновесие.
Частным видом относительного движения является относительное равновесие (покой). Условия, при которых имеет место равновесие точки выражаются теоремой:
“Для относительного равновесия свободной точки необходимо и достаточно, чтобы она первоначально покоилась и чтобы равнялась нулю равнодействующая действительных сил и переносной силы инерции”
![]() ,
, ![]() .
(31.17)
.
(31.17)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.