и, кроме того, в начальный момент
времени заданы координаты и скорости точки, определяющие ее начальное состояние при ![]() ,
, ![]() ,
, ![]()
![]() .
(25.3)
.
(25.3)
Задача состоит в том, чтобы по этим данным определить движение точки относительно декартовой системы, т.е. найти функции
![]()
![]() .
(25.4)
.
(25.4)
2°. Существование и единственность решения.
Для решения обратной задачи воспользуемся дифференциальными уравнениями движения точки в декартовых координатах
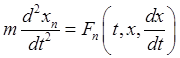
![]() .
(25.5)
.
(25.5)
Так как масса
и сила заданы, то ![]() и
и ![]() известные
величины. Следовательно, уравнения (25.5) являются системой трех
дифференциальных уравнений второго порядка, в которых неизвестными функциями
являются координаты точки
известные
величины. Следовательно, уравнения (25.5) являются системой трех
дифференциальных уравнений второго порядка, в которых неизвестными функциями
являются координаты точки ![]() . Величины (25.3)
определяют начальные условия для этой системы. Тем самым, обратная задача сводится
к начальной задаче (Задаче Коши):требуется определить систему трех функций
. Величины (25.3)
определяют начальные условия для этой системы. Тем самым, обратная задача сводится
к начальной задаче (Задаче Коши):требуется определить систему трех функций ![]() , удовлетворяющих системе дифференциальных
уравнений (25.5) и начальным условиям (25.3).
, удовлетворяющих системе дифференциальных
уравнений (25.5) и начальным условиям (25.3).
Если расширить
число искомых функций, добавив к координатам ![]() еще и
скорости
еще и
скорости ![]() , то эту задачу можно представить в виде
начальной задачи для нормальной системы шести уравнений:
, то эту задачу можно представить в виде
начальной задачи для нормальной системы шести уравнений:
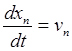 ,
, 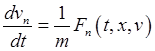 ,
,
![]() ,
, ![]() ,
, ![]()
![]() .
(25.6)
.
(25.6)
Условия на силы (25.2)
обеспечивают непрерывность по времени правых частей уравнений и их принадлежность
к классу Липшица по искомым функциям. Следовательно, выполнены условия теоремы
о существовании и единственности решения задачи Коши (25.6) в некоторой
окрестности начальных данных. Поэтому существует единственный набор функций ![]() ,
, ![]() ,
удовлетворяющих и уравнениям, и начальным условиям (25.6). Эти функции и
определяют движение точки.
,
удовлетворяющих и уравнениям, и начальным условиям (25.6). Эти функции и
определяют движение точки.
Заметим, что разрешимость задачи Коши, вообще говоря, не означает возможность получения решения в виде аналитической формулы: достаточно табличного представления функций. Аналитическое представление решения, тем не менее, возможно при частном виде сил (что будет продемонстрировано в дальнейшем). Кроме того, всегда можно решить задачу приближенно на основе методов численного интегрирования уравнений и получить решение с требуемой степенью точности.
3°. Роль начальных условий.
Система трех
дифференциальных уравнений второго порядка (25.5) имеет шестой порядок. Из
теории дифференциальных уравнений известно, что общее решение такой системы
содержит шесть произвольных постоянных ![]() :
:
![]()
![]() .
(25.7)
.
(25.7)
Наличие в правых частях этих уравнений произвольных параметров означает, что под действием данной силы точка совершает не какое-то одно движение, а целый класс движений. Как показывает опыт, точка под действием силы движется по-разному в зависимости от ее исходного состояния. Так, например, под действием веса тело может двигаться прямолинейно или криволинейно, смотря по тому, была ли вертикальной или на наклонной к горизонту его начальная скорость.
Таким образом, одних дифференциальных уравнений еще не достаточно для однозначного определения движения. Чтобы сделать обратную задачу динамики определенной, нужны дополнительные условия, которые позволили бы выделить из класса возможных движений фактически реализуемое движение. Роль таких условий и играют начальные условия (25.3), задающие начальное положение и начальную скорость точки.
Начальные условия позволяют найти постоянные интегрирования в (25.7) и тем самым конкретизировать движение. Действительно, взяв производные по времени от функций (25.7), получим скорости
![]()
![]() .
(25.8)
.
(25.8)
Подставив затем в (25.7) и (25.8)
начальные данные (25.3), получим шесть уравнений для шести постоянных ![]() :
:
![]() ,
, ![]()
![]() .
(25.9)
.
(25.9)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.