Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 3

Рис.1

(здесь и далее индекс принимает значения 1,2,3). С геометрической точки зрения равенства (2.1) представляют собою уравнения трех плоскостей, называемых координатными. Тем самым, положение точки в пространстве определяется пересечением трех координатных плоскостей (Рис.1).

Каждая пара координатных плоскостей (2.1), пересекаясь, определяет прямую линию, называемую координатной:

пересечение плоскостей , определяет-прямую                               (2.2)

(индекс ограничен числом 3). Через каждую точку пространства проходят три координатные прямые (Рис.1).

В прямоугольной декартовой системе координат во всех точках пространства параллельны друг другу, как одноименные координатные плоскости, так и одноименные координатные прямые. Кроме того, в каждой точке взаимно ортогональны как координатные плоскости так и координатные прямые, при этом координатные прямые ортогональны одноименным координатным плоскостям.

3°. Координатный базис.

С каждой точкой  пространства связывают тройку единичных векторов-ортов , направленных вдоль координатных прямых в сторону возрастания координат. Векторы  некомпланарны: построенный на них (как на ребрах) параллелепипед имеет ненулевой объем: .

Тройка независимых векторов  определяет так называемый координатный базис. Элементы базиса в силу свойств координатной системы обладают рядом свойств: они не меняются от точки к точке, представимы друг через друга, единичны и взаимноортогональны:

,           ,                                                                     (2.3)

(– символ Кронекера). Таким образом, в прямоугольной декартовой системе координат базис постоянен и ортонормирован.

4°. Представление вектора в декартовом базисе.

Пусть в точке приложен вектор . Согласно правилу параллелепипеда этот вектор можно представить в виде результирующего трех составляющих векторов , идущих вдоль координатных линий и коллинеарных ортам соответствующих осей:  (Рис.2). Таким образом:

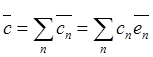.                          (2.4)

Рис.2

Формула (2.4) дает разложение вектора в декартовом базисе. В этом разложении величины  называют декартовыми компонентами вектора.

Компоненты представимы через скалярные произведения самого вектора и элементов базиса:

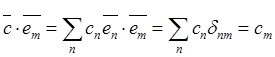,                                                                                      (2.5)

т.е. равны проекциям вектора на соответствующие оси. Согласно (2.5) нулевой вектор  имеет нулевые компоненты: .

Свойство разложения вектора (2.4) выражает теорема: “Разложение вектора в координатном базисе единственно”. Доказательство: Допустим противное: пусть, наряду с (2.4) имеет место и другое разложение вектора 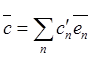, где хотя бы для одного  выполнено условие . Тогда вычитаем различные представления вектора и получаем равенство 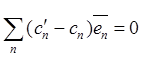. Отсюда в силу независимости базисных векторов должны равняться нулю все коэффициенты при них: , что и противоречит исходному допущению. Это противоречие доказывает теорему.

Компоненты определяют как модуль, так и направление вектора. Действительно, с учетом свойства ортонормированности базиса (2.3) и представления компонент вектора (2.5) справедливы соотношения:

,

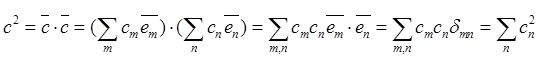, откуда модуль и направление вектора определяются в виде:

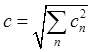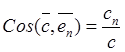,          .                                                                                      (2.6)

5°.Годограф вектора.

Пусть в точке  приложен переменный вектор . Для него вводят в рассмотрение вспомогательное трехмерное пространство , вдоль декартовых осей  с ортами  которого отсчитываются переменные компоненты вектора (Рис.3). Тогда вектор , откладываемый от начала , изобразится вектором , который через составляющие векторы  и через компоненты  может быть представлен в виде разложений:

.              (2.7)