Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 12

Движение точки можно определить заданием ее траектории (с помощью двух функций , ) и уравнением движения по траектории (с помощью функции ). Тем самым естественное задание движения точки выражается тремя функциями

,      ,      .                                                                                   (9.10)

(вместо последнего уравнения часто используется обратное равенство ). Далее полагаем эти функции принадлежащими следующим классам: , .

3°. Естественное вычисление скорости точки.

При движении точки  по траектории ее вектор-радиус является сложной функцией времени . Дифференцируя эту зависимость по времени и используя определение скорости, найдем

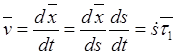.                                                                                                       (9.11)

С другой стороны, вектор скорости можно выразить разложением в естественном базисе . Сопоставление этих формул в силу единственности разложения требует совпадения одноименных компонент:

,      ,      .                                                                                             (9.12)

Отсюда следует, что скорость направлена по касательной в траектории (Рис.12), а ее модуль совпадает с абсолютным значением ненулевой компоненты

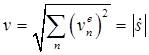.                                                                                                             (9.13)

В частности, при , .

4°. Определение движения точки по траектории по ее скорости и начальному положению.

Пусть задана скорость  и начальное положение точки . Тогда представляя равенство  в форме  и интегрируя с учетом начального положения, получаем уравнение движения точки по траектории

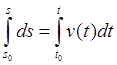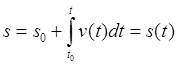,        .                                                                       (9.14)

Т.е. скоростью и начальным положением уравнение движения точки полностью определяется.

5°. Естественное вычисление ускорения точки.

Ускорение точки является производной по времени от ее скорости. Поэтому, дифференцируя по времени выражение (9.11) скорости и используя первую формулу в (9.5), найдем

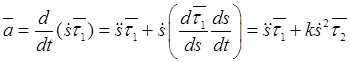.                                                                     (9.15)

С другой стороны, для вектора ускорения в естественном базисе справедливо разложение . Из этих двух разложений в силу единственности находим

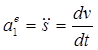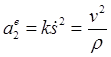,      ,      .                                                                        (9.16)

Составляющие ускорения вдоль естественных осей

,      ,     

называют соответственно касательным, нормальным и бинормальным ускорениями. Поскольку бинормальное ускорение равно нулю, ускорение точки складывается из касательного и нормального ускорений (Рис.12)

Рис.12

.                                                (9.17)

Из вывода формулы (9.15) для ускорения ясно, что касательное ускорение характеризует изменение скорости по величине, а нормальное ускорение – изменение скорости по направлению.

В соответствии с формулами для произвольного вектора модуль ускорения его естественными компонентами определяется в виде

.                                                                    (9.18)

Направление ускорения, принадлежащего соприкасающейся плоскости, удобно определять углом  между главной нормалью и ускорением (Рис.12)

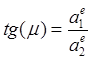.                                                                                                                        (9.19)

6°. Определение скорости точки по касательному ускорению и начальной скорости.

Пусть, наряду с траекторией, задано касательное ускорение  и начальная скорость . Тогда из выражения , представленного  в форме  в результате интегрирования с учетом начальной скорости получим скорость движения по траектории

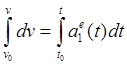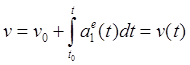,      .                                                                    (9.20)

Тем самым касательным ускорением и начальной скоростью скорость движения по траектории полностью определяется.

7°. Круговое движение точки.