Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 19

Поскольку векторы  и  параллельны друг другу, смешанное произведение обращается в ноль, а скалярные произведения дают проекции скоростей на :

, , , поэтому равенство принимает вид

.                                                                                                             (12.3)

Формула (12.3) выражает теорему: «В произвольном движении твердого тела проекции скоростей двух его точек на соединяющую эти точки прямую равны друг другу».

Умножим, далее, скалярно обе части равенства (12.2) на орт  угловой скорости , в результате будем иметь

.

Векторы  и  параллельны друг другу, поэтому смешанное произведение равно нулю, скалярные же произведения дают проекции скоростей на :

, , .

В итоге приходим к соотношению

,                                                                                                            (12.4)

выражающему теорему: «В произвольном движении твердого тела проекции скоростей двух его точек на направление угловой скорости тела равны друг другу».

3°. Вычисление скоростей точек тела.

Для определения скорости типичной точки тела установим выражения ее компонент в подвижном базисе. Представив входящие в выражение скорости (12.1) векторы в подвижном базисе :

,    ,    ,

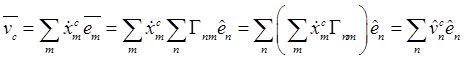, будем иметь

    (индекс ).                                                                     (12.5)

Здесь  – заданы, они определяют точку  тела,  – компоненты угловой скорости, определяемые по формулам Эйлера , а  – компоненты скорости полюса, определяемые по уравнениям движения тела  в виде .

Компонентами (12.5) скорость точки в подвижных осях координат определяется в виде

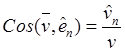,    .                                                                                (12.6)

Скорость точки можно определить и по ее компонентам в неподвижном базисе. Для этого входящие в выражение скорости (12.1) векторы представим в неподвижном базисе :

,    ,    ,

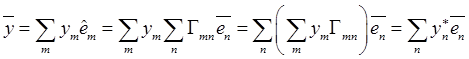, тогда из (12.1) будем иметь

    (индекс ).                                                                     (12.7)

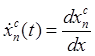Здесь  – компоненты скорости полюса (определяемые по уравнениям движения полюса ),  – компоненты угловой скорости тела, определяемые формулами Эйлера , а  – компоненты вектора  в неподвижном базисе, имеющие значения,  (из равенства  можно также получить ).

Компонентами (12.7) скорость точки в неподвижных осях координат определяется в виде

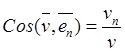,    .                                                                                (12.8)

13. Ускорение точки твердого тела.

Получим формулы, позволяющие по уравнениям движения твердого тела определить ускорение любой его точки.

1°. Представление ускорения точки тела.

Ранее показано, что скорость любой точки тела , выражаемая через скорость полюса  и угловую скорость тела , является переменным вектором

.                                          (13.1)

Темп изменения скорости характеризуется ускорением, являющимся производной по времени от вектора скорости 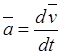. Покажем, что ускорение подобно скорости может быть представлено через характеристики движения полюса и вращения тела вокруг полюса.

Дифференцируя по времени равенство (13.1), находим

.

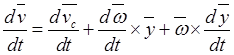Производные по времени от векторов в этом равенстве имеют значения

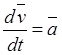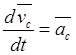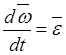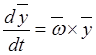,   ,   ,   , поэтому равенство принимает вид

,                                                                                               (13.2)

где  есть угловое ускорение тела. Это равенство и определяет ускорение типичной точки твердого тела в произвольном движении. Выясним механический смысл членов, входящих в его правую часть.

Первый член  является ускорением полюса. Во втором члене  представим вектор-радиус  через две составляющие  и , одна из которых параллельна угловому ускорению, а вторая ортогональна ему:

,   ,   ,

Тогда

   .                                                                    (13.3)

Следовательно, этот член выражает собою касательное ускорение точки  при ее вращении вокруг вектора , проведенного из полюса (Рис.26а). Последний член в (13.2)  представим по формуле векторной алгебры в виде