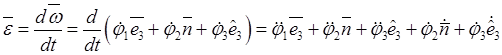Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 18

.                                    (11.18)

Векторы

,    ,                                                                                        (11.19)

называют соответственно угловыми ускорениями прецессии, нутации и собственного вращения. Получим выражения для двух последних членов в (11.18). На основании представления  и Формул Пуассона (11.16) получаем:

, , поэтому

,                                           (11.20)

Подстановка (11.19), (11.20) в (11.18) приводит к  представлению углового ускорения через скорости и ускорения прецессии, нутации и собственного вращения

.                                                                    (11.21)

Для вычисления углового ускорения тела получим выражения для его компонент в подвижных и неподвижных осях. Дифференцируя по времени представление угловой скорости в подвижных осях  и используя формулы Пуассона, получим

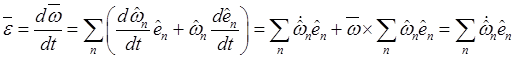, так как

.

С другой стороны, в подвижном базисе . Из этих двух представлений  в подвижном базисе следует, что должно быть

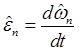
    ,                                                                                                  (11.22)

т.е. компоненты углового ускорения в сопутствующих осях равны производным по времени от соответствующих компонент угловой скорости в тех же осях. Так как согласно формулам Эйлера  выражаются через , то согласно (11.22) компоненты  будут функциями . То есть уравнения вращения тела вокруг полюса  определяют как угловую скорость, так и угловое ускорение тела.

По компонентам (11.22) модуль и направление углового ускорения определяются формулами

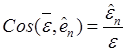
,     .                                                          (11.23)

Для вычисления углового ускорения тела в системе отсчета, возьмем представление  в неподвижном базисе . После дифференцирования по времени этого равенства получим

.

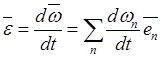Отсюда и из представления углового ускорения в неподвижном базисе  следуют выражения для его компонент

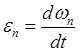
    .                                                                                                  (11.24)

Т.е. подобно (11.22) компоненты углового ускорения в неподвижном базисе равна производным по времени от соответствующих компонент угловой скорости.

Формулы (11.24) определяют угловое ускорение тела в неподвижных осях в виде

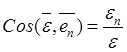, .                                                              (11.25)

12. Скорость точки тела.

1°. Представление скорости типичной точки тела.

Движение тела в системе отсчета  определяется уравнениями , . Покажем, что эти уравнения дают возможность вычислить скорость любой точки  тела. Как следует из Рис.23 для типичной точки  тела вектор-радиус  складывается из вектор-радиуса полюса  и вектор-радиуса относительно полюса :

.

Дифференцируя по времени это равенство, найдем

.

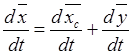Согласно определению скорости первые два члена равенства равняются скоростям точек  и :

,    .

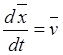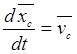Что касается последнего члена, то с помощью формул Пуассона он может быть представлен в виде

.

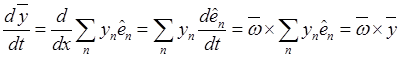Подставляя значения производных в исходную формулу, получим

.                                                                                                      (12.1)

В равенстве (12.1) вектор  является скоростью полюса, а вектор  - является скоростью точки  относи при ее вращении вокруг мгновенной оси , проходящей через полюс (ее называют скоростью вращения вокруг полюса).

Таким образом (12.1) выражает следующую теорему:

«Если тело совершает произвольное движение, то скорость его типичной точки равна векторной сумме скорости полюса и скорости вращения вокруг полюса.» (Рис.23)

2°. Свойства скоростей точек тела.

Пусть  – две произвольные точки тела и  – скорости точек в рассматриваемый момент (Рис.24). Беря точку  за полюс, для скорости точки  согласно (12.1) получим представление

.                                                      (12.2)

Умножим скалярно обе части этого равенства на орт  вектора :

, тогда получим

.