Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 55

Для потенциальной силы мощность равна производной по времени от взятой со знаком “минус” потенциальной энергии:

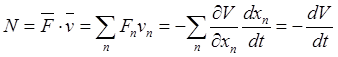,                                                                     (30.22)

а работа – разности значений потенциальной энергии в начальной и конечной точках пути

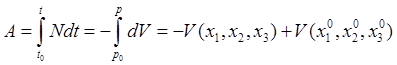.                                                         (30.23)

Следовательно, эта работа не зависит от формы пути.

Рассмотрим теорему о кинетической энергии (30.14) при действии на точку потенциальной силы; тогда в силу (30.22) будем иметь

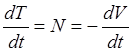 или .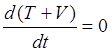

Отсюда следует, что имеет место интеграл энергии

.                                                                                                           (30.24)

Сумму  кинетической и потенциальной энергий называют механической энергией точки. Равенство (30.24) выражает закон сохранения механической энергии: “При движении точки под действием потенциальной силы ее механическая энергия сохраняет постоянное значение”.

Потенциальность сил реализуется в достаточно широком классе задач. Таковы, например, сила тяготения, сила упругости и т.п.

Если помимо потенциальных сил на точку действуют и непотенциальные силы, например, силы сопротивления, то механическая энергия не сохраняется, а переходит в другие формы энергии, например, в тепловую энергию. Процессы, в которых такой переход имеет место, называют диссипативными. В земных условиях в силу неизбежного сопротивления движению диссипация механической энергии происходит всегда, поэтому говорить о законе сохранения энергии в этом случае можно только в известном приближении.

6°. Движение тяжелой точки по гладкой полусфере.

Применение теоремы о кинетической энергии проиллюстрируем следующим примером. Пусть тело  веса , находившееся на вершине гладкой полусферы радиуса , получив скорость , пришло в движение. Определим точку  (угол ) схода тела со сферы, а также минимальное значение скорости , при которой тело сразу покинет полусферу (Рис.72).

Тело движется под действием веса и нормальной реакции сферы по меридиану, плоскость которого содержит начальную скорость.

Точка схода характеризуется тем условием, что в ней обращается в нуль давление на полусферу, а, следовательно, и реакция полусферы. Нормальную реакцию можно выразить через скорость движения из дифференциального уравнения в проекцию на главную нормаль траектории:  в виде

,       .

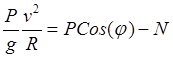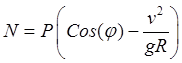
Для точки схода  будем иметь

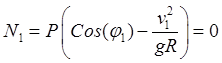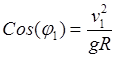,   .                                                                 (30.25)

Скорость в точке схода можно определить путем применения теоремы о кинетической энергии к пути  вдоль окружности (Рис.72): . Входящие в теорему величины имеют значения

,   ,      ,

,

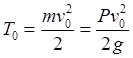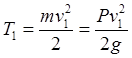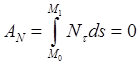
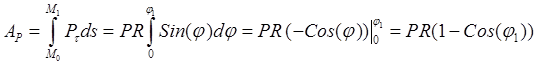Следовательно, теорема определяет  в виде

,   .

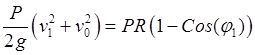Подстановка выражения для  в (30.25) приводит к уравнению для косинуса угла точки схода, определяющего угол в виде

,   .

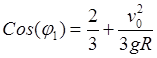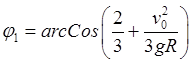Минимальная скорость , при которой тело сразу покидает купол, соответствует нулевому значению угла  . Эта скорость находится из уравнения

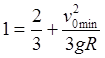
и имеет значение .

Глава Динамика Относительного движения точки.

Ньютоновские законы механики справедливы не в любой, а только в инерциальной системе отсчета. Однако, инерциальные системы далеко не исчерпывают всех возможных систем. В ряде случаев важно знать движение точки относительно системы отсчета, не являющейся инерциальной, которая, в свою очередь, может произвольно двигаться относительно инерциальной системы. Такое движение тела называют относительным. Важной задачей динамики поэтому является установление основного закона механики в относительном движении.

31. Основной закон динамики относительного движения.

Покажем, что в относительном движении (движении в инерциальной системе отсчета) основному закону динамики можно придать вид закона движения в инерциальной системе, если к обычным силам добавить специальные силы – силы инерции.

1°. Вывод основного закона.