|
 При движении точки в системе отсчета
При движении точки в системе отсчета 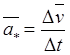 ,
характеризующий изменение скорости за время
,
характеризующий изменение скорости за время 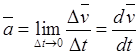 .
(5.1)
.
(5.1)
Таким образом, ускорение является вектором, равным производной по времени от вектора скорости. Ускорение точки направлено в сторону вогнутости траектории (Рис.7).
Для вычисления
ускорения представим скорость в координатном базисе ![]() . дифференцируя
по времени это равенство, согласно (5.1) будем иметь
. дифференцируя
по времени это равенство, согласно (5.1) будем иметь
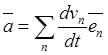 .
(5.2)
.
(5.2)
С другой
стороны, ускорение через свои компоненты представимо разложением ![]() . В силу единственности разложения вектора должны
совпадать коэффициенты при элементах базиса
. В силу единственности разложения вектора должны
совпадать коэффициенты при элементах базиса
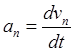 ,
, ![]() ,
(5.3)
,
(5.3)
т.е. компоненты ускорения равны производным по времени от соответствующих компонент скорости.
Каждое из
слагаемых в (5.2) можно рассматривать как ускорение ![]() точки
точки ![]() – проекции
– проекции ![]() на ось
на ось ![]() вдоль этой оси. Тем самым ускорение
пространственного движения точки равно результирующей ускорений в трех
составляющих движениях вдоль координатных осей.
вдоль этой оси. Тем самым ускорение
пространственного движения точки равно результирующей ускорений в трех
составляющих движениях вдоль координатных осей.
По известным компонентам (5.3) модуль и направление вектора ускорения определяются известными формулами
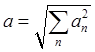 ,
, 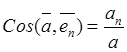 ,
, ![]() . (5.4)
. (5.4)
2°. Определение скорости точки по ускорению.
По ускорению и
начальной скорости можно определить скорость точки. Пусть заданны в любой
момент времени ускорение ![]() и начальная скорость
и начальная скорость![]() точки. Тогда, интегрируя зависимости
точки. Тогда, интегрируя зависимости ![]() , представленные в форме
, представленные в форме ![]() , будем иметь
, будем иметь
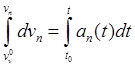 ,
, 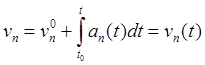 .
(5.5)
.
(5.5)
Формулы (5.5) определяют скорость точки в любой момент.
6. Условия попадания снаряда в самолет.
1°. Постановка задачи.
Рассмотрим задачу об условиях попадания зенитного снаряда в самолет, рассматриваемых как точечные тела.
 Пусть
самолет
Пусть
самолет ![]() летит равномерно и прямолинейно со скоростью
летит равномерно и прямолинейно со скоростью
![]() на высоте
на высоте ![]() над землей
и в момент
над землей
и в момент ![]() пролетает над орудием
пролетает над орудием ![]() . С какой начальной скоростью
. С какой начальной скоростью ![]() и под каким углом
и под каким углом ![]() к
горизонту должен вылететь снаряд
к
горизонту должен вылететь снаряд ![]() , движущийся с
ускорением свободного падения
, движущийся с
ускорением свободного падения ![]() , чтобы попасть в самолет?
, чтобы попасть в самолет?
Возьмем орудие
за начало системы отсчета ![]() с осью
с осью ![]() , направленной вдоль движения самолета, и
осью
, направленной вдоль движения самолета, и
осью ![]() , идущей вертикально вверх через начальное
положение
, идущей вертикально вверх через начальное
положение ![]() самолета (Рис.8).
самолета (Рис.8).
|
Составим
уравнения движения самолета и снаряда в системе ![]() . По
известной скорости и начальному положению самолета
. По
известной скорости и начальному положению самолета ![]() :
:
![]() ;
; ![]() , в результате интегрирования
равенств
, в результате интегрирования
равенств ![]() :
:
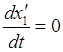 ,
, 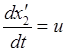 ,
, 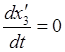 , с учетом начального положения
, с учетом начального положения ![]() получаем уравнения движения самолета
получаем уравнения движения самолета
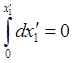 ,
, 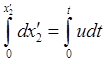 ,
, 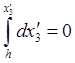 ;
;
![]() ,
, ![]() ,
, ![]() .
(6.1)
.
(6.1)
Т.е. самолет
летит в вертикальной плоскости ![]() . Траекторией самолета
служит горизонтальная прямая
. Траекторией самолета
служит горизонтальная прямая ![]() :
: ![]() ,
, ![]() (Рис.8).
(Рис.8).
Примем, что
начальная скорость ![]() снаряда принадлежит вертикальной
плоскости
снаряда принадлежит вертикальной
плоскости ![]() и составляет угол
и составляет угол ![]() с
горизонтальной осью
с
горизонтальной осью ![]() . Тогда по известному ускорению и
начальной скорости снаряда
. Тогда по известному ускорению и
начальной скорости снаряда ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.