Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 42

Решение системы существует, ибо ее функциональный определитель отличен от нуля

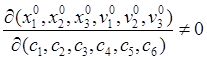
(равенство нулю определителя означало бы, что независимые друг от друга начальные координаты и скорости оказались бы зависимыми величинами). Решив эту систему, определяем постоянные через начальные координаты и скорости

    .                                                                                           (25.10)

Подстановка постоянных (25.10) в (25.7) приводит к частному решению уравнений (25.5), удовлетворяющему начальным условиям (25.3)

    .                                                                                        (25.11)

Таким образом, дифференциальные уравнения совместно с начальными условиями определяют единственное движение точки.

Рассмотрим ряд примеров решения обратной задачи динамики, представляющих и самостоятельный интерес.

4°. Движение под действием восстанавливающей силы.

Рассмотрим прямолинейное движение точки  массы  под действием восстанавливающей силы , направленной к неподвижному центру  этой прямой и пропорциональной расстоянию до этого центра. Эта сила стремится вернуть точку в положение  (где сила равна нулю), т.е. восстановить положение равновесия. К числу таких сил относится, например, упругая сила.

Беря прямую, вдоль которой происходит движение, за ось  с началом в точке , примем, что в начальном положении  точка имела координату  и скорость , направленную вдоль прямой  (Рис.52). Произвольному моменту времени соответствует положение  точки с координатой . Определим движение точки, т.е. функцию .

Дифференциальное уравнение движения точки вдоль оси :  в данном случае имеет вид . Упрощая уравнение и присоединяя к нему начальные условия, получим начальную задачу

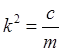,   , при ,   ,   .                                                                                  (25.12)

Действующая сила  непрерывно-дифференцируема по координате, следовательно, начальная задача (25.12) имеет единственное решение. Так как (25.12) – линейное однородное уравнение второго порядка, то его решение является линейной комбинацией двух частных решений :

,   ,   .

Беря в качестве частных решений , , будем иметь

.                                                                                                 (25.13)

Если вместо  ввести новые постоянные , то общее решение можно представить в компактной форме

,   ,

.                                                  (25.14)

Так как координата точки является периодической функцией, то движение имеет колебательный характер с амплитудой , круговой частотой  и начальной фазой . Это движение называется собственным колебанием точки.

Постоянные интегрирования  находятся из уравнений, получаемых подстановкой начальных условий (25.12) в формулы

, , и имеют вид , . Следовательно, амплитуда  и начальная фаза  согласно (25.14) равны

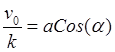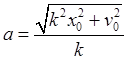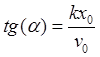,   ;    ,   .                               (25.15)

Из равенств

,  

и (25.14) заключаем, что координата точки находится в пределах , т.е. график функции (25.14) находится между двумя прямыми  и , называемыми амплитудными прямыми (Рис.53).

Заметим, что если учесть силу сопротивления, пропорциональную скорости и направленную против движения:  , то характер движения изменится. Можно показать, что вместо гармонического колебания движение станет затухающим колебанием, заключенным между амплитудными кривыми ,   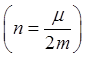и имеющим вид, указанный на рисунке 54.

5°. Движение под действием восстанавливающей и возмущающей сил.

Пусть на точку  вдоль оси , наряду с восстанавливающей силой , действует возмущающая периодическая сила . Установим движение точки в этом случае из начального положения  с начальной скоростью , направленной вдоль оси (Рис.55).

Дифференциальное уравнение движения вдоль оси :  в данном случае будет вида . После упрощения и присоединения к нему начальных условий приходим к начальной задаче

,   ,   ;

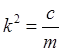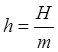при ,   ,   .                   (25.16)