Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 52

Принцип Даламбера в некоторых случаях позволяет сводить задачу динамики к задаче статики. Это имеет место при решении прямой задачи, т.е. задачи определения силы по заданному движению. При решении же основной задачи динамики об определении движения по заданной силе изложенный метод лишь упрощает составление уравнения движения; необходимость интегрирования этих уравнений, конечно, сохраняется.

3°. Форма свободной поверхности жидкости во вращающемся сосуде.

Применим принцип Даламбера к определению формы свободной поверхности жидкости во вращающемся сосуде.

Пусть сосуд в форме круглого цилиндра с вертикальной осью вращается вокруг этой оси с постоянной угловой скоростью  вместе с находящейся в нем жидкостью. При этом, как показывают наблюдения, поверхность жидкости не остается горизонтальной: на ней образуется некоторое углубление (Рис.70). Определим форму свободной поверхности жидкости  относительно неподвижной системы координат  с началом  в центре основания сосуда, осью , направленной по оси сосуда вертикально вверх, и осями , , проведенными в горизонтальной плоскости (Рис.70).

Возьмем частицу  жидкости с массой  на поверхности жидкости. На нее действует сила тяжести , направленная вертикально вниз и равная , и реакция поверхности , направленная по нормали к ней:  (принимается, что жидкость не препятствует скольжению частиц вдоль свободной поверхности, т.е. что эта поверхность гладкая). Приложим еще к этой частице ее силу инерции , равную . Тогда, согласно второй форме принципа Даламбера, будем иметь условие равновесия сил:

.

Учитывая выражения для сил, отсюда получим векторное и соответственно компонентные уравнения несвободного движения частицы

;

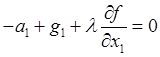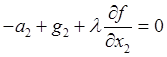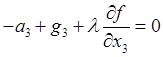,   ,   .                                 (29.8)

Так как с каждой прямой, параллельной оси , поверхность жидкости пресекается в одной точке, уравнение поверхности можно искать в виде, разрешенном относительно координаты. ___________________________ Тогда будем иметь

,   ,   ,   .

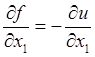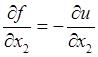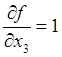Компоненты ускорения свободного падения имеют значения

,   ,   .

При установившемся вращении цилиндр и жидкость можно рассматривать как единое твердое тело, равномерно вращающееся вокруг своей оси со скоростью . В этом вращении уравнения движения частицы  и компоненты ее ускорения соответственно равны

,   ,      ,

,   ,   .

Подставив значения компонент векторов в уравнения (29.8), получим соотношения

,   ,   .

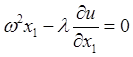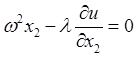Эти равенства определяют множитель связи и частные производные функции  в виде

,   ,   .

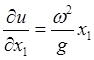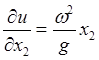Теперь легко видеть, что

.

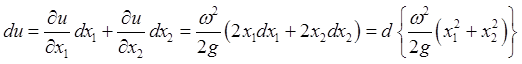Следовательно,

,   .

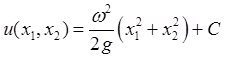Обозначим через  точку, в которой ось вращения пересекает поверхность жидкости (Рис.70), и через  – расстояние . Тогда точка  имеет координаты . Из условия того, что свободная поверхность  проходит через эту точку, находим: .

Итак,

.

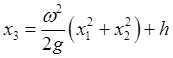Установленное равенство представляет собой уравнение параболоида вращения с вершиной в точке  и осью . Таким образом, поверхность жидкости во вращающемся сосуде принимает форму параболоида вращения с осью, идущей вдоль оси сосуда (Рис.70).

30. Общие теоремы динамики точки.

Из основного закона динамики можно установить соотношения, связывающие меры движения точки с мерами силового воздействия на точку, которые называют общими теоремами динамики. Эти теоремы в ряде случаев дают интегралы дифференциальных уравнений движения.

1°. Меры движения.

Пусть точка  массы , движущаяся относительно инерциальной системы отсчета , в момент времени  занимает положение  с вектор-радиусом  и имеет скорость  (Рис.71).

За векторные меры движения (меры Декарта) принимают величины

,   ,                                          (30.1)

называемые количеством движения и кинетическим моментом (относительно центра ). Вектор  характеризует запас движения, которым обладает точка, а вектор  – меру ее вращения вокруг начала отсчета . Эти меры сохраняют свои значения при инерционном движении точки. Из (30.1) следует, что , т.е. кинетический момент связан с секторной скоростью.