Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 33

.                                                                                                                   (20.16)

Здесь компоненты  определяются согласно уравнениям движения среды  по формулам Эйлера (первого типа) , компоненты же  определяются согласно уравнениям движения тела относительно среды  по формулам Эйлера (второго типа) .

По компонентам (20.16) величина абсолютной угловой скорости тела и ее ориентация относительно системы  определяются формулами

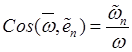
,       .                                                     (20.17)

3°. Сложение угловых ускорений тела.

При сложном движении твердого тела между его абсолютным угловым ускорением и угловыми ускорениями относительного и переносного движений (как и между обычными ускорениями в сложном движении точки) существует определенная зависимость. Эта зависимость устанавливается теоремой сложения угловых ускорений тела.

Теорема: “Если твердое тело совершает сложное движение, то в каждый момент времени его абсолютное угловое ускорение равно векторной сумме переносного, относительного и добавочного угловых ускорений”:

,    .                                                                                       (20.18)

Доказательство. Возьмем выражение  абсолютной угловой скорости тела и вычислим от него абсолютную производную по времени

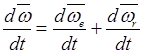.                                                                                                            (20.19)

Установим выражения для каждой из производных, входящих в это равенство. Согласно определениям абсолютного и переносного угловых ускорений имеем

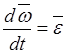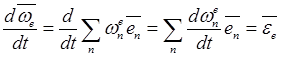
,       .                                           (20.20)

Из второго в (20.20) равенства заключаем, что относительное движение тела не влияет на его переносную угловую скорость (угловую скорость среды ).

Для абсолютной производной по времени от относительной угловой скорости имеем представление

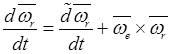.                                                                                                      (20.21)

Первый  вектор в правой части равенства согласно определению является относительным угловое ускорением тела : 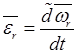; он характеризует изменение относительной угловой скорости  относительно среды (в системе ).

Второй вектор правой части  определяет изменение вектора , обусловленное движением (вращением) среды ; его обозначают через  и называют добавочным угловым ускорением: . Тем самым, формуле (20.21) можно придать вид

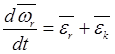.                                                                                                                  (20.22)

Подстановка выражений (20.20) и (20.22) в (20.19) приводит к зависимости , которая и доказывает теорему (20.18).

Формула (20.18) геометрически означает, что абсолютное угловое ускорение тела является замыкающей ломаной линии, звеньями которой служат переносное, относительное и добавочное угловые ускорения (Рис.48).

Для аналитического определения абсолютного углового ускорения тела достаточно установить выражения для его компонент в неподвижной или одной из подвижных систем координат.

Вектор абсолютного углового ускорения (20.18)

в базисе  сопутствующей системы  имеет компоненты:

     (индекс),                                                           (20.23)

где

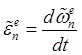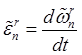,    ,    ,    .                                       (20.24)

По компонентам (20.23) модуль и направление углового ускорения относительно осей  определяются в виде

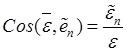
,       .                                                        (20.25)

4°. Движение мельничного бегуна.

Ось  мельничного бегуна  вращается равномерно вокруг вертикальной оси  с угловой скоростью . Длина оси , радиуса бегуна  (Рис.49).

Считая, что бегун катится без скольжения, определить его угловую скорость и угловое ускорение.

Возьмем неподвижную систему  с вертикальной осью  и горизонтальными осями ,  и свяжем с осью  бегуна (средой ) подвижную систему , направив ось  по оси бегуна, ось  – по вертикали, а ось  – ортогонально к ним.