Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 5

Введем величину, характеризующую темп и направление изменения точки в пространстве. Будем считать, что движение точки  в системе отсчета  задано векторным уравнением  (Рис.5). Пусть в соседние моменты времени  и  точка занимает на траектории положения  и , определяемые вектор-радиусами  и  соответственно. Тогда за время  точка получает перемещение, приближенно выражаемое приращением вектор-радиуса . Отношение 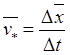, характеризующее средний темп и направление движения за время , называют средней скоростью точки за этот промежуток. Средняя скорость является вектором, направленным по хорде  в сторону движения. Приближенность вектора  состоит в том, что переменное движение точки

Рис.5

вдоль дуги  заменяется равномерным движением вдоль хорды . Ясно, однако, что чем меньше промежуток , тем меньше, вообще говоря, различие между хордой и дугой и тем точнее средняя скорость характеризует истинный темп и направление движения. Поэтому за скорость  точки в данный момент  принимают предел, к которому стремится средняя скорость при стремлении к нулю времени движения, т.е. производную

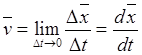.                                                                                                                (4.1)

Таким образом, скорость точки в данный момент есть вектор, равный производной по времени от ее вектор-радиуса. Так как в пределе при  точка  и направление хорды  определяет направление касательной к кривой, то скорость  направлена по касательной к траектории точки в сторону ее движения.

Для вычисления скорости используем разложение вектор-радиуса в координатном базисе . Дифференцирование по времени этого равенства в силу определения (4.1) скорости дает

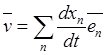.                                                                                                                       (4.2)

С другой стороны вектор скорости через свои компоненты представим выражением . В силу единственности разложения компоненты разложений должны совпадать:

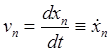
       .                                                                                             (4.3)

Т.е. проекции скорости на декартовы оси равны производным по времени от соответствующих координат точки.

В выражении (4.2) слагаемое  определяет скорость движения точки  (проекции  на ось ). Следовательно, согласно (4.2) скорость пространственного движения точки оказывается равной результирующей скоростей трех составляющих движений вдоль координатных осей. По известным компонентам (4.3) модуль и направление вектора скорости определяются известными формулами

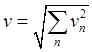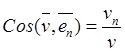,          .                                                                                      (4.4)

2°. Годограф скорости.

Во вспомогательном трехмерном пространстве  с декартовой системой  – пространстве годографа скорости вектор , откладываемый от неподвижного центра  в разные моменты времени, опишет кривую линию – годограф скорости (Рис.6). Зависимости компонент скорости от времени

                       (4.5)

являются параметрическими уравнениями годографа скорости.

3°. Определение уравнений движения точки по скорости.

Рис.6

По скорости и начальному положению можно найти движение точки. Пусть в любой момент времени известна скорость точки  и ее начальное положение . Тогда выражения для скоростей (4.3) , записанные в форме , после интегрирования дают зависимости

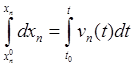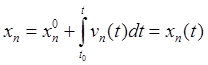,             ,                                                          (4.6)

являющиеся уравнениями движения. Тем самым скоростью и начальным положением движение точки полностью определено.

5. Вектор ускорения точки.

1°. Определение ускорения точки по скорости.