Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 16

. (10.3)

В силу уравнений движения тела (10.1) и формул (10.3) величины , суть заданные функции времени. Поэтому для точки тела функции (10.3) представляют собою координатные уравнения движения. Так как координаты могут быть любыми, то (10.3) дают уравнения движения любой точки тела.

11. Угловая скорость и угловое ускорение тела.

Движение тела относительно системы отсчета складывается из движения вместе с полюсом и вращения вокруг полюса. В первом движении ориентация тела сохраняется неизменной; темп этого движения характеризуется скоростью и ускорением полюса. Во втором движении полюс неподвижен, а ориентация тела изменяется. Введем величины (угловую скорость и угловое ускорение), характеризующие темп изменения ориентации.

1°. Элементарное перемещение точки в круговом движении.

При движении точки по окружности радиуса (Рис.19) ее скорость представляется в виде

(11.1)

где – вектор-радиус, лежащий в плоскости окружности, вектор угловой скорости радиуса, направленный по оси вращения с ортом , ортогональной плоскости окружности, а – угол поворота радиуса вокруг оси. Введем вместо другой вектор для точки , отсчитываемый от точки оси, и представим его в виде суммы двух составляющих, коллинеарной и ортогональной оси

, , .

Тогда будем иметь а для скорости (11.1) получим представление

, . (11.2)

С другой стороны, скорость точки относительно центра можно выразить в виде производной 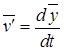, поэтому

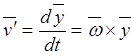Отсюда следует, что элементарное перемещение точки при круговом движении можно записать в виде

. (11.3)

Отсюда видно, что вектор направлен по касательной к окружности в сторону вращения.

2°. Угловая скорость тела.

Вращение тела вокруг полюса является результирующим трех вращений: прецессионного – вокруг оси с угловой скоростью , нутационного – вокруг линии узлов с угловой скоростью и собственного – вокруг оси с угловой скоростью . Все три оси пересекаются в полюсе и в каждом из вращений у типичной точки тела один и тот же вектор-радиус (Рис.20).

В результате каждого составляющего вращения точка получает свое элементарное перемещение, которое согласно (11.3) можно записать в виде

, , .

Результирующее элементарное перемещение точки равно векторной сумме составляющих перемещений

(11.4)

Выражение (11.4) того же типа, что и элементарное перемещение (11.3) при вращательном движении. Следовательно, результирующее движение также является вращательным, происходящим с угловой скоростью :

(11.5)

вокруг оси , идущей в направлении . Вектор называют угловой скоростью тела, а ось , вдоль которой он направлен – мгновенной осью вращения. Согласно (11.5) угловая скорость тела является векторных суммой угловых скоростей прецессии, нутации и собственного вращения.