Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 13

К числу простейших движений точки относится круговое движение – движение по окружности.

Пусть окружность радиуса  с центром в точке  расположена в плоскости, параллельной плоскости  декартовой системы  (Рис.13), а  – движущаяся по ней точка. Установим уравнения движения точки.

Рис.13

Положение радиуса  определяется углом , который он составляет с радиусом . Зависимость  называют уравнением вращения радиуса. Далее принимается, что .Темп изменения угла, характеризуемый производной от него по времени, обозначается через :

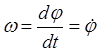                                                                                                                        (9.21)

и называют угловой скоростью радиуса. Темп изменения угловой скорости, обозначаемый , определяется производной

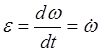.                                                                                                                       (9.22)

Рассматривают также векторы угловой скорости и углового ускорения, определенные формулами

,                                                                                             (9.23)

и направленные по оси вращения (Рис.13).

Уравнение движения точки по окружности имеет вид

.                                                                                                                      (9.24)

Если использовать параметрические уравнения окружности (Рис.13)

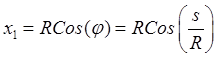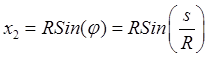,    ,    , то производные по дуге от координат будут равны

,         ,         ,

,    ,   

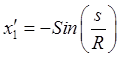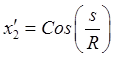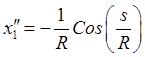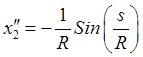и кривизна окружности будет постоянной, обратной радиусу, а радиус кривизны равен радиусу окружности

,               .

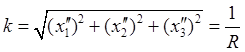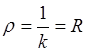Кручение окружности – плоской линии равно нулю: . Тем самым, естественные уравнения окружности имеют вид

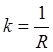,      .                                                                                                               (9.25)

Формулы (9.24) и (9.25) дают естественное представление движения по окружности.

Естественный базис окружности в типичной точке  ориентирован следующим образом. Орт касательной  направлен по касательной в сторону возрастания дуги, орт главной нормали  направлен по радиусу окружности к ее центру, а орт бинормали  совпадает с ортом  (Рис.13).

Естественная компонента скорости согласно (9.24) равна произведению радиуса окружности на его угловую скорость

.                                                     (9.26)

Рис.14

Вектор скорости точки , направленный по касательной к окружности, может быть представлен через радиус-вектор точки и угловую скорость вращения (Рис.14)

,           .                                  (9.27)

Касательное ускорение равно произведению радиуса на угловое ускорение:

.                                                                                                              (9.28)

Вектор касательного ускорения, направленный по касательной к окружности, может быть выражен через радиус-вектор и угловое ускорение вращения (Рис.14)

Рис.14

.                                                              (9.29)

Нормальное ускорение равно произведению радиуса на квадрат угловой скорости:

.                                                                                                                  (9.30)

Вектор нормального ускорения, направленный вдоль радиуса к центру окружности, может быть выражен через радиус-вектор и квадрат угловой скорости (Рис.14):

.                                                                                (9.31)

Вектор полного ускорения точки, равный векторной сумме касательного и нормального ускорений, имеет выражение

.                                                                                                 (9.32)

Модуль и направление вектора ускорения в круговом движении его естественными компонентами (9.28) и (9.30) определяются в виде