Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 60

При свободном падении точка движется под действием веса и Кориолисовой силы инерции. Уравнение движения имеет вид

,   ,  

или

,   .

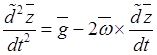В подвижной системе отсчета  это векторное уравнение эквивалентно трем скалярным уравнениям

,(, индекс).

Если учесть значения компонент векторов

,,;,,,,, то уравнения движения примут вид

,   ,   .                 (32.12)

Требуется найти решение этой системы уравнений, отвечающее следующим начальным условиям:

,   ,   ;   .                                                             (32.13)

Уравнения (32.12) после интегрирования дают

,   ,   , где  – произвольные постоянные. Начальными условиями (32.13) эти постоянные определяются в виде

,   , поэтому предыдущие формулы принимабт вид

,   ,   .     (32.14)

Определив  из первого уравнения

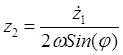                                                                                                                 (32.15)

и подставив его в третье уравнение, получаем уравнение, допускающее интегрирование

.

Интегрируя и определяя произвольную постоянную с помощью условий (32.13), найдем

.

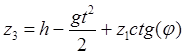Подстановка (32.15) и (32.16) во второе уравнение в (32.14) приводит к уравнению для координаты

.                                                                                              (32.17)

Это – линейное неоднородное уравнение второго порядка. Его общее решение имеет структуру

,                                                                                                        (32.18)

где  – частное решение уравнения (32.17),  – произвольные постоянные, а ,  – частные решения однородного уравнения . Легко проверить, что его решениями будут , .

Решение  ищем в виде квадратичного полинома времени. Тогда

,   ,   .

Подстановка этих величин в (32.17) приводит к соотношению

, выполняющемуся при

,   ,   , т.е. при

,   ,   .

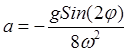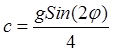Следовательно,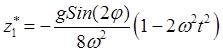

и общее решение (32.18) будет

.

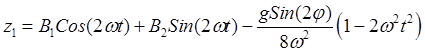Постоянные  определяются условиями (32.13) в виде

,

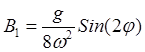и координата  будет следующей функцией времени

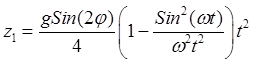.                                                                                      (32.19)

Подстановка  в (32.15) и (32.16) дает зависимость от времени остальных координат

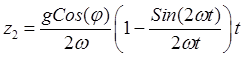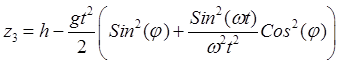,   .               (32.20)

Форлулы (32.19), (32.20) дают уравнения падения точки. Из них следует, что при падении точка отклоняется как в южном, так и в восточном направлениях. Кроме того, поскольку 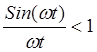, она несколько замедляет свое падение. На полюсах

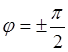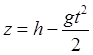,   ,   , т.е. падение происходит строго по вертикали. На экваторе

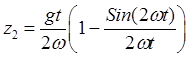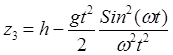,   ,   ,   , т.е. имеется только восточное отклонение.

Для оценки отклонений от вертикали в произвольных широтах разложим тригонометрические функции в сходящиеся ряды по степеням малой величины:  и ограничимся двумя первыми членами разложений; тогда получим

,,

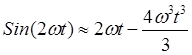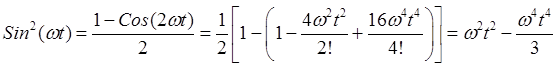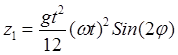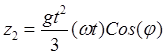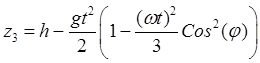,   ,   .        (32.21)

Из (32.21) (ввиду ) видно, что южное отклонение  является малой величиной высшего порядка сравнительно с восточным отклонением . Пренебрегая в (32.21) членами, содержащими , с достаточной точностью будем иметь

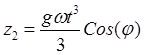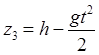,   ,   .                                                                      (32.22)

Таким образом, в даннлм приближении падающая точка отклоняется только к востоку. Установим теперь зависимость отклонения от высоты падения. Для этого, положив , найдем время падения: 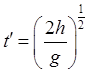. Подстановка  в формулу для  дает искомую величину отклонения

.

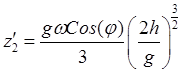В частности, при падении с высоты м на широте , где м/с², получаем

мм.

Таким образом, восточное отклонения оказывается достаточно заметным, чтобы быть обнаруженным в эксперименте. Многочисленные опыты подтвердили наличие восточного отклонения, близкого к теоретическому значению. Эти эксперименты могут служить подтверждением вращения Земли.