Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 48

Таким образом, согласно (27.7)-(27.10) полная реакция связи определяется выражением

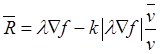.                                                                                                         (27.11)

При  поверхность называют шероховатой, а при  – гладкой. Реакция шероховатой поверхности имеет нормальную и тангенциальную составляющие; реакция же гладкой поверхности – только нормальную составляющую.

Реакция связи (контактная сила) по своей природе несколько отличаются от других сил (сил дальнодействия), которые называют активными силами. Отличие состоит в том, что реакция не вполне определяется связью; она зависит также от других сил и от движения точки. При отсутствии активных сил и движения реакция вообще не появляется: при  и  будем иметь:

,   ,   ,   .

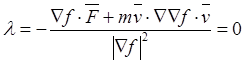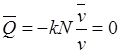Кроме того, активные силы, действуя на покоящуюся точку, могут сообщить ей движение (отсюда и название "активные"), реакции же этим свойством не обладают, поэтому их называют еще пассивными силами. Реакция связи наперед неизвестна и подлежит определению.

Итак, при движении по поверхности основной закон механики имеет вид

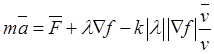,                                                                                              (27.12)

где

,   .

4°. Уравнения движения и начальная задача.

Пусть точка  массы  движется по поверхности  относительно декартовой системы координат . В проекциях на оси этой системы векторный основной закон (27.12) эквивалентен системе трех скалярных уравнений движения по поверхности (называемых уравнениями Лагранжа со множителем связи); присоединив к ним уравнение связи, получим систему четырех уравнений

   ,

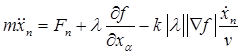
   (,  ).                   (27.13)

для определения четырех функций времени . Эти функции входят в уравнения неравноправно: относительно  система дифференциальная, а относительно  – алгебраическая, т.е. (27.13) является системой уравнений смешанного типа. Присоединив к ней начальные условия (для функций ):

,   ,      ,                                                                 (27.14)

получим начальную задачу. Условия (27.14) полагаются согласованными с уравнением связи и ограничением на скорость:

,   .

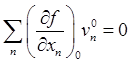Начальную задачу для смешанной системы решают путем сведения ее к начальной задаче для дифференциальной системы. Для этого из уравнения связи множитель связи находят в виде функции времени, координат и скоростей (27.9):

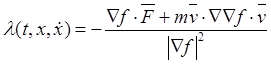,                                                                                  (27.15)

в результате чего первые три уравнения в (27.13) составят систему одних дифференциальных уравнений для неизвестных . Записав ее в виде уравнений для шести функций  :

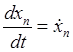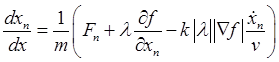
,      ,                                         (27.16)

и используя условия (27.14), получим начальную задачу для нормальной системы.

Пусть заданы масса , коэффициент трения , компоненты силы  как непрерывно дифференцируемые функции переменных  и уравнение связи  как трижды непрерывно дифференцируемая функция координат. Тогда множитель связи  будет непрерывно дифференцируемой функции , а вместе с ним из этого же класса будут и правые части уравнений. Следовательно, задача (27.16), (27.14) имеет единственное решение .

По известному движению согласно (27.15) определяется , а, следовательно, и реакция (27.11). Таким образом, основной задачей динамики несвободной точки является определение не только движения, но и реакции связи.

5°. Движение тяжелой точки по гладкой наклонной плоскости.

Проиллюстрируем стесненное движение точки следующим примером.

Пусть тяжелая точка  массы  движется по гладкой наклонной плоскости, составляющей с плоскостью горизонта угол , из заданного начального состояния. Определим движение точки и реакцию плоскости в декартовой системе координат , оси  которой принадлежат плоскости (ось  – горизонтальна), а ось  – ортогональна к ней (Рис.64).

В этих координатах уравнение гладкой плоскости и ее градиент имеют вид