Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 31

8°. Движение кольца по вращающемуся стержню.

Применение теоремы Кориолиса проиллюстрируем на примере движения кольца по вращающемуся стержню.

Путь кольцо  движется по горизонтальному стержню , вращающемуся вокруг вертикальной оси, проходящей через его точку . Требуется определить ускорение кольца относительно земли.

Свяжем неподвижную систему  с землей, а подвижную систему  – со стержнем  (играющим роль среды ) так, чтобы их третьи оси совпадали, а ось  была направлена по стержню (Рис.44). Движения кольца и стержня заданы уравнениями

,   ,   ;

,   ,   ,   , где функции

В относительном движении кольца  (по оси ) векторное уравнение движения, скорость и ускорение равны

,   ,   .

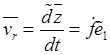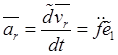В переносном движении (движении стержня) полюс  неподвижен

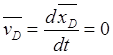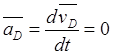,   ,   , а угловая скорость и угловое ускорение стержня параллельны друг другу и направлены по оси вращения

,       .

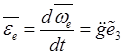
Следовательно, переносное ускорение равно

,

,    .

Кориолисово ускорение имеет значение

.

Абсолютное ускорение кольца согласно теореме Кориолиса определяется выражением

, где компоненты в подвижной системе равны

,   ,   .

Следовательно, его компоненты определяют величину и направление абсолютного ускорения относительно подвижных осей  в виде

,

,   ,   .

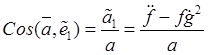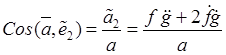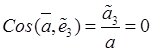Таким образом, абсолютное ускорение кольца ортогонально оси вращения, т.е. принадлежит плоскости вращения стержня.

20. Сложное движение тела.

Рассмотрим сложное движение твердого тела.

1°. Сложение движений тела.

Пусть дано относительное и переносное движения тела  и требуется определить его абсолютное движение. Относительное движение – движение тела  по отношению к среде  (в системе  (Рис.45)) определяется уравнениями

,    ,    .                    (20.1)

Здесь первые три уравнения определяют движение полюса  относительно среды , а последние три уравнения – ориентацию осей , связанных с телом, относительно осей , связанных со средой. При этом относительные скорость и ускорение полюса  определяются формулами

,   ;    ,   ,   ,                                 (20.2)

а относительные угловая скорость и угловое ускорение – в виде

,   ;    ,   ,   .                         (20.3)

Переносное движение – движение среды  относительно тела отсчета  (в системе  (Рис.45)) определяется уравнениями

,    ,    .                                                                         (20.4)

где первая тройка уравнений дает движение полюса  среды относительно “неподвижного” тела , а вторая тройка – определяет ориентацию осей , связанных со средой, относительно “неподвижных”осей . При этом переносные скорость и ускорение полюса  определяются формулами

,   ;    ,   ,   ,                                (20.5)

а переносные угловая скорость и ускорение среды – в виде

,   ;    ,   ,   .                        (20.6)

Выразим абсолютные координаты тела  через заданные величины (20.1) и (20.4). Введём соотношение между вектор-радиусами точек  и  (Рис.45):

                                                                                                                        (20.7)

и представим входящие в него векторы в базисе неподвижной системы отсчёта. Имеем

,   ,   .

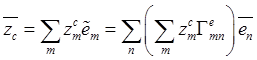Подстановка этих представлений в (20.7) приводит к равенствам

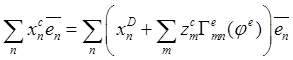, из которых для абсолютных координат полюса  с учетом (20.1) и (20.4) находим выражения

    ,                                                                 (20.8)

определяющие абсолютное движение полюса .

Для получения уравнений абсолютного вращения тела  вокруг полюса  рассмотрим различные представления для ортов  сопутствующих осей . Разлагая эти орты в базисе неподвижной системы, находим

.

С другой стороны, эти же разложения можно получить другим путем, используя формулы:

,   ,    .

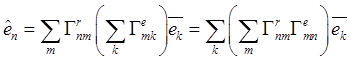Из полученных двух разложений вектора  в базисе  следует равенство одноименных компонент

,                                                                                                       (20.9)