![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() .
.
Путем интегрирования зависимостей
![]() :
:
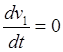 ,
, 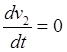 ,
, 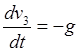
с учетом начальной скорости получим скорость снаряда
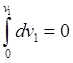 ,
, 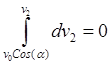 ,
, 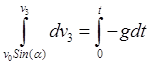 ;
;
![]() ,
, ![]() ,
, ![]() .
.
По найденной
скорости снаряда и его начальному положению ![]() в
результате интегрирования равенств
в
результате интегрирования равенств ![]() :
:
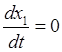 ,
, 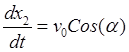 ,
, 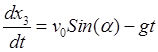
получаем уравнения движения снаряда
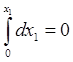 ,
, 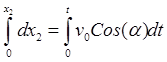 ,
, 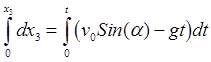 ;
;
![]() ,
, ![]() ,
, 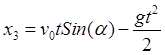 .
(6.2)
.
(6.2)
Таким образом, снаряд движется в
вертикальной плоскости ![]() и его траекторией служит
парабола
и его траекторией служит
парабола 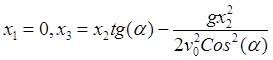 .
.
3°. Условия попадания.
Для попадания
снаряда в самолет требуется совпадение их координат (6.1) и (6.2) в некоторый
момент ![]() :
: ![]() , что
приводит к условиям
, что
приводит к условиям
![]() ,
, 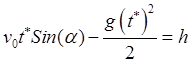 , которые после упрощений принимают
вид
, которые после упрощений принимают
вид
![]() ,
, ![]() .
(6.3)
.
(6.3)
Согласно первому из них
горизонтальная скорость снаряда должна совпадать со скоростью самолета. Второе
условие является квадратным уравнением для времени встречи ![]() . Решая его, получаем два момента
. Решая его, получаем два момента
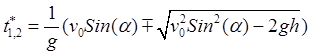 .
.
Условием попадания снаряда в самолет является действительность этих корней, т.е. неотрицательность дискриминанта
![]() .
(6.4)
.
(6.4)
Из первого в (6.3) условия
следуют выражения: 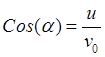 ,
, 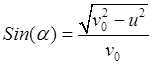 ,
определяющие угол
,
определяющие угол ![]() в виде
в виде 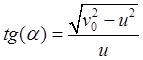 .
С учетом значения
.
С учетом значения ![]() второе условие (6.4) для
начальной скорости дает выражение
второе условие (6.4) для
начальной скорости дает выражение![]() , определяющее ее в
виде
, определяющее ее в
виде ![]() . Таким образом, решение задачи имеет вид
. Таким образом, решение задачи имеет вид
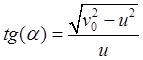 ,
, ![]() , т.е. угол возвышения орудия
должен иметь определенное значение, а начальная скорость не должна быть меньше
некоторого значения; эти значения определяются исходными данными движения тел.
, т.е. угол возвышения орудия
должен иметь определенное значение, а начальная скорость не должна быть меньше
некоторого значения; эти значения определяются исходными данными движения тел.
При минимальных значениях начальной скорости и угла
![]() ,
, 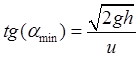
моменты встречи ![]() и
и ![]() совпадают,
т.е. траектория
совпадают,
т.е. траектория ![]() снаряда касается траектории
снаряда касается траектории ![]() самолета (Рис.8). При
самолета (Рис.8). При ![]() ,
, ![]() будем
иметь
будем
иметь ![]() и траектория
и траектория ![]() снаряда
дважды пересечет траекторию
снаряда
дважды пересечет траекторию ![]() самолета. Если же
самолета. Если же ![]() ,
, ![]() , то моменты
встречи
, то моменты
встречи ![]() ,
, ![]() становятся
комплексными. Это означает, что снаряда не попадет в самолет , их траектории не
пересекутся. В этом случае траектория
становятся
комплексными. Это означает, что снаряда не попадет в самолет , их траектории не
пересекутся. В этом случае траектория ![]() снаряда
проходит ниже траектории
снаряда
проходит ниже траектории ![]() самолета, не достигая
ее.
самолета, не достигая
ее.
7. Ортогональная криволинейная система координат.
Помимо прямоугольной декартовой системы координат для представления движения точки относительно тела отсчета может быть использована произвольная криволинейная координатная система. В классической механике обычно используют ортогональные криволинейные системы. Рассмотрим особенности таких систем.
1°. Координатные поверхности и линии.
Рассмотрим представления
декартовых координат точки через три независимых параметра ![]() :
:
![]()
![]() .
(7.1)
.
(7.1)
Относительно функций
![]() предполагаем, что они однозначны и трижды
непрерывно-дифференцируемыми в области изменения параметров и что отличен от
нуля определитель третьего порядка – якобиан
предполагаем, что они однозначны и трижды
непрерывно-дифференцируемыми в области изменения параметров и что отличен от
нуля определитель третьего порядка – якобиан
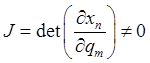 .
(7.2)
.
(7.2)
Условие (7.2)
означает, что зависимости (7.1) могут быть обращены, т.е. величины ![]() можно выразить как функции переменных
можно выразить как функции переменных ![]() :
:
![]()
![]() .
(7.3)
.
(7.3)
 Задание
тройки чисел
Задание
тройки чисел ![]() означает в силу (7.1) задание декартовых
координат
означает в силу (7.1) задание декартовых
координат ![]() и тем самым фиксирование некоторой точки
пространства. Обратно, каждой точке пространства соответствует три декартовых
координаты
и тем самым фиксирование некоторой точки
пространства. Обратно, каждой точке пространства соответствует три декартовых
координаты ![]() , а в силу (7.3) и три числа
, а в силу (7.3) и три числа ![]() . Тем самым между тройкой величин
. Тем самым между тройкой величин ![]() и точкой пространства существует взаимно
однозначное соответствие, что позволяет называть
и точкой пространства существует взаимно
однозначное соответствие, что позволяет называть ![]() обобщенными
координатами. Каждое из уравнений
обобщенными
координатами. Каждое из уравнений
![]()
![]() (7.4)
(7.4)
геометрически определяет некоторую
криволинейную поверхность, называемую координатной. Пересечение трех координатных
поверхностей определяет в пространстве точку ![]() (Рис.9).
(Рис.9).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.