Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 24

Согласно (16.14) ускорение точки плоской фигуры равно векторной сумме ускорения полюса, сложенного с касательным и нормальным ускорениями при ее вращении вокруг полюса (Рис.33).

Для вычисления ускорения точки в подвижных осях установим его компоненты в этой системе. Согласно (16.14) и (16.15) имеем

,,.(16.16)

Здесь согласно (16.7), (16.13) и (16.15) компоненты ,  и  равны

,   , ;

,   ,   ,   ,   , а компоненты ускорения полюса имеют значения :

,    ,    .

С учетом полученных выражений компоненты (16.16), модуль и направление ускорения относительно подвижных осей определяются формулами

,

,

;                                                                                                                              (16.17)

,         ,  ,  .

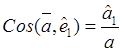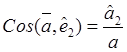Аналогично вычисляется ускорение точки в неподвижных осях. В этих осях согласно (16.14) и (16.15) получаем

,,. (16.18)

Здесь согласно (16.7), (16.13) и (16.15) компоненты , ,  и  в неподвижной системе равны :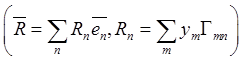

,   ,   ;      ,   ,

,,,

,   ,   .

Следовательно, компоненты (16.18) модуль и направление ускорения точки относительно неподвижных осей выражаются формулами

,

,

;                                                                                                                              (16.19)

,         ,  ,  .

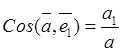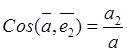Согласно формулам (16.16) (или (16.19)), ускорение точки, подобно скорости, лежит в плоскости ее движения.

5°. Карданово движение плоской фигуры.

В качестве примера плоского движения рассмотрим карданово движение. Кардановым называют такое движение плоской фигуры, при котором две ее точки  и  перемещаются по двум взаимно ортогональным прямым.

Примем эти прямые за оси  и  системы отсчете (Рис.34). Пусть точка  движется по оси , а точка  – по оси . Обозначим через  неизменное расстояние между точками. Примем за полюс  фигуры  середину отрезка  и направим сопутствующие оси фигуры , ортогонально этому отрезку и вдоль него. Тогда уравнения движения фигуры  примут вид

,   ,   ,                                                                   (16.20)

где  – произвольная функция. Тем самым, из трех функций , , , определяющих плоское движение, в кардановом движении, независима только одна.

Рассмотрим движение произвольной точки  фигуры и установим вид ее траектории. Общие уравнения движения точки фигуры в данном случае принимают вид

,

.                                      (16.21)

Для получения уравнения траектории в явном виде достаточно из этих уравнений исключить параметр . С этой целью вначале разрешим уравнения относительно синуса и косинуса

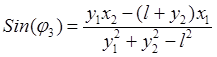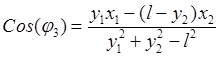,   , а затем исключим угол  с помощью тождества :

.                                              (16.22)

Полученное уравнение можно представить в форме

,                                                                                                  (16.23)

где

,   ,   ,   .                     (16.24)

Отсюда видно, что траекторией точки служит центральная кривая второго порядка. Для определения ее вида составим дискриминант уравнения

.

Для точек фигуры, не лежащих на окружности :

,                                                                                                                     (16.25)

дискриминант отрицателен, следовательно траекторией точки является эллипс. Центр этого эллипса находится в начале координат (поскольку уравнение траектории не содержит членов первой степени относительно ), a оси симметрии эллипса в силу  повернуты на некоторый угол относительно координатных осей.

В частной случае, когда точка  принадлежит отрезку , имеем  и уравнение эллипса (16.22) принимает вид

.

Его, очевидно, можно представить в форме

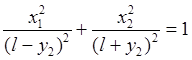, откуда следует, что осями симметрии эллипса являются координатные оси, а полуосями служат величины  и .

В другом частном случае, когда точка  лежит на окружности , уравнение траектории (16.22) будет иметь вид

.                                                                   (16.26)