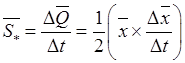Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 44

, называют средней секторной скоростью радиус-вектора точки за время . Величина  – приближенная, но это приближение тем точнее, чем меньше время . Поэтому за меру темпа роста площади в рассматриваемый момент  принимают предел , к которому стремится средняя секторная скорость при стремлении к нулю времени движения, т.е. производную

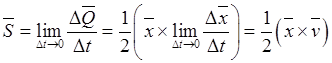.                                                                        (26.1)

Секторную скорость можно вычислять в любой системе координат. В частности, в цилиндрической системе  с базисом  векторы  и компоненты  имеют выражения

,   ,   ;

,   ,   .                                                                         (26.2)

В частном случае движения точки в плоскости  будем иметь  и компоненты секторной скорости (26.2) будут равны

,   ,   ,                                                                                        (26.2)

т.е. в этом случае секторная скорость ортогональна плоскости движения: .

2°. Плоскость движения. Законы площадей.

Пусть точка  массы  (планета) движется под действием силы тяготения к центру  из заданного начального состояния. В инерциальной системе отсчета  с началом в центре  сила тяготения выражается в ви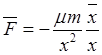де , где  – вектор-радиус точки, а начальное состояние определяется начальными вектор-радиусом  и скоростью  (Рис.60). Установим вначале вид траектории точки.

Возьмем дифференциальное уравнение движения в векторном виде

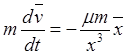                                                                                                                  (26.4)

и умножим векторно слева обе его части на ; в результате (после сокращения на массу) получим

.

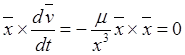Отсюда следует векторный интеграл уравнения движения, называемый интегралом площадей

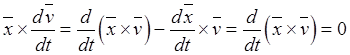,   ,   .                            (26.5)

Векторная постоянная, равная удвоенной секторной скорости, определяется начальным состоянием точки:

.                                                                                                                (26.6)

Умножив интеграл (26.5) скалярно на , устанавливаем, что координаты точки удовлетворяют уравнению плоскости , проходящей через начало отсчета ортогонально вектору  (Рис.61)

,   .                                                                    (26.7)

Формулы (26.5), (26.7) выражают первый закон Кеплера: “Все планеты описывают вокруг солнца плоские орбиты, следуя закону площадей”.

3°. Определение орбиты.

Дальнейшее решение задачи удобно производить в полярных координатах , выбранных на плоскости  так, чтобы полюс совпадал с центром , а полярный угол отсчитывался от оси  (Рис.61). В этих координатах компоненты силы и начальное состояние определяются величинами

,   ;

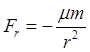при ,   ,   ,   ,   ,                               (26.8)

где  – угол между перпендикуляром к начальному вектор-радиусу и начальной скоростью.

Из дифференциальных уравнений в полярных координатах

,                                                                                  (26.9)

в силу второго условия в (26.8) следует равенство

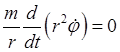, которое после интегрирования определяет скалярный интеграл площадей

,   .                                                            (26.10)

Интеграл площадей позволяет выразить производную по времени через производную по полярному углу:

,   ,

,  

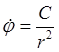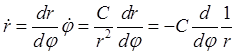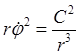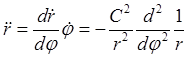
и представить первое равенство в (26.9) в виде так называемой формулы Бине

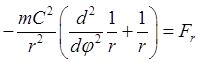.                                                                                                 (26.11)

Подставляя в нее из (26.8) радиальную силу, получим после упрощений дифференциальное уравнение траектории – орбиты

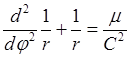.                                                                                                               (26.12)

Это уравнение является линейным неоднородным уравнением второго порядка для обратного радиуса . Частным решением уравнения является постоянная 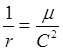. Для однородного уравнения  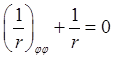частными решениями являются функци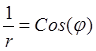и  и 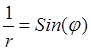, а общим решением – их линейная комбинация 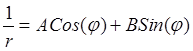. Следовательно, общее решение уравнения (26.12) имеет вид