2. Объясните понятие «структурная схема системы». Изобразите структурную схему ПИ-регулятора.
3. Какими свойствами обладают системы управления с П- и ПИ-регуляторами?
4. Объясните понятие «управляемость системы». Дайте определение критерия управляемости Калмана.
5. Объясните понятие «наблюдаемость системы». Дайте определение критерия наблюдаемости Калмана.
6. Объясните понятие «статическая погрешность системы управления». Как вычислить статическую погрешность системы управления с известной передаточной функцией?
7. Объясните понятие «устойчивая система». Дайте определение критерия устойчивости линейной непрерывной системы.
8. Объясните понятие «неустойчивая система». Дайте определение критерия неустойчивости линейной непрерывной системы.
9. Объясните понятие «система находится на границе устойчивости». Дайте определение критерия нейтральной (критической) линейной непрерывной системы.
10. Как составить характеристическое уравнение системы с известной передаточной функцией?
Пример программы вычисления по уравнениям (f), (g), (l), (4) массивов
значений переменных состояния 
и 
:
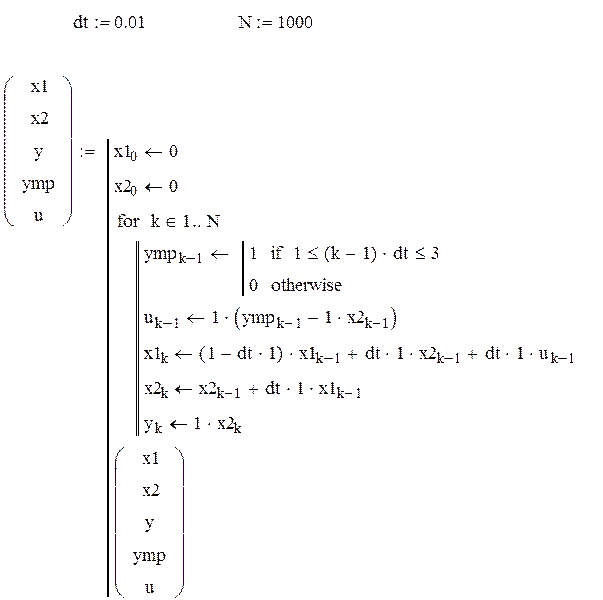
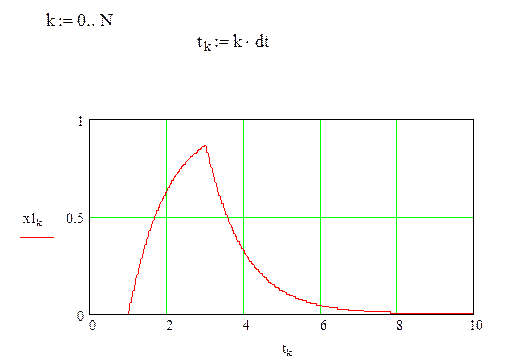
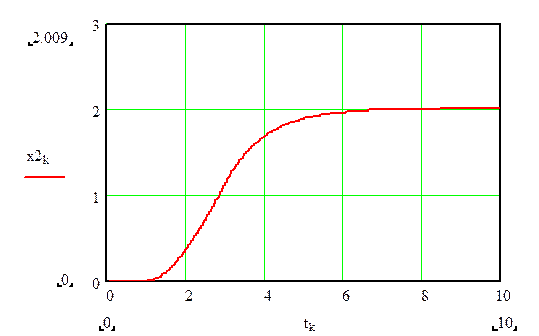
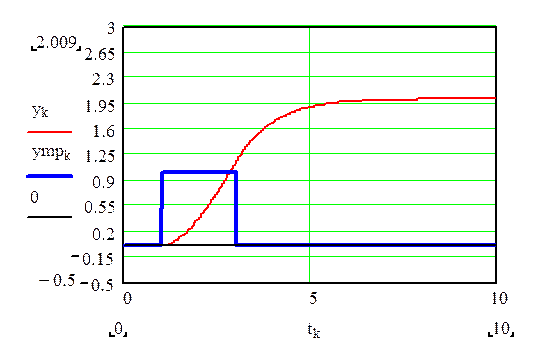
Из сравнения графиков изменения переменных 
и 
(реализованного
и требуемого изменения выходного сигнала объекта управления) подтверждают
сделанный ранее вывод о том, что эту систему по назначению применять нельзя.
Лабораторная работа № 3.
ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
1. Методические указания
Понятие "стохастический
процесс" довольно сложно. Чтобы прийти к его правильному пониманию,
выдающимся ученым потребовалась не одна сотня лет. Окончательно понятие
стохастического процесса было сформулировано в работе А. Н. Колмогорова
в 1930 г. Стохастический процесс (случайный процесс, случайная функция) можно
рассматривать как семейство стохастических переменных 
Стохастические
переменные индексируются параметромt, который принадлежит
множеству Т, называемому множеством индексов. В теории стохастического
управления он интерпретируется как время. Таким образом, Т - это множество
действительных переменных. В случае дискретных стохастических систем множествоТ - это совокупность моментов квантования, т. е. Т =
{ ..., -h, 0, h, ...}, или T = { ..., -1, 0, 1, ...}, если период
квантования h равен единице.
Случайный процесс можно рассматривать как функцию x(t, u) двух переменных. Для фиксированного u= u0 функция x (· , u0) сводится к обычной функции времени, называемой реализацией При фиксированном t = t0функция x (t0, ·) есть случайная величина. Следовательно, можно считать. что случайный процесс вырабатывается генератором случайных сигналов. Аргумент u при записи частот опускают.
Полностью детерминированные стохастические процессы. Одна из возможностей получения случайного процесса заключается в том, чтобы задать в качестве начального условия для обыкновенного дифференциального уравнения случайную величину и, решая его, генерировать функции времени. Однако случайные процессы данного типа малоинтересны, поскольку они “недостаточно случайны”. Это становится очевидным при анализе случайного процесса, вырабатываемого интегратором со случайными начальными условиями. Так как выход интегратора постоянен, то
x (t, u) - x (t - h, u) = 0
для всех t, h и u. Такой стохастический процесс называется полностью детерминированным процессом, потому что его будущие значения могут быть точно определены по его прошлому.
Вообще говоря, случайный процесс x(t u), называют полностью детерминированным, если l{x (t, u)} = 0 почти для всех u(здесь l{ }- произвольный линейный оператор, не тождественно равный нулю). Это значит, что полностью детерминированные случайные процессы можно прогнозировать с помощью линейного предиктора почти для всех u(почти всеuозначает всеu, кроме возможного множества точек с мерой нуль).
Основные понятия теории случайных процессов. Значения случайного процесса вn различных моментов времени представляют собой n-мерные случайные величины. Функция
|
|
(1) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
