Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 64

и исследовать его корни l_k  (k = 1, 2, ..., n).

А. М. Ляпунов доказал две теоремы, которые позволяют исследовать все случаи первой категории.

Теорема 1. Если вещественные части всех корней l_k характеристического уравнения (6.9) первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво независимо от членов разложения выше 1-го порядка малости.

Теорема 2. Если среди корней l_k характеристического уравнения (6.9) первого приближения найдется по меньшей мере один с положительной частью, то невозмущенное движение неустойчиво независимо от членов разложения выше 1-го порядка малости.

Критические случаи имеют место, когда среди всех корней l_k уравнения (6.9) имеется некоторая группа корней, вещественная часть которых равна нулю, а остальная группа корней имеет отрицательную вещественную часть. В критических случаях вопрос об устойчивости невозмущенного движения (6.6) не может быть разрешен на основании исследования уравнений первого приближения. В критических случаях устойчивость (неустойчивость) невозмущенного движения определяется видом нелинейных функций F_k. Поэтому в приведенных случаях необходимо рассматривать уравнения (6.9) в их исходном виде.

Характеристическое уравнение, соответствующее системе уравнений (6.8), имеет вид

Пусть для определенности все корни уравнения (6.10) различны, тогда решение уравнения

где l₁, l₂, l₃, ..., l_n - корни характеристического уравнения; A₁, A₂, A₃, ..., A_n - постоянные интегрирования, зависящие от начальных условий.

Пусть далее l_k - вещественный корень. Если l_k> 0, то член  с течением времени непрерывно возрастает и стремится к бесконечности. В этом случае x также стремится к бесконечности и система неустойчива.

Если l_k< 0, то член с течением времени стремится к нулю (затухает). Пусть один из корней l_r - комплексный, тогда всегда существует сопряженный с ним :

l_r = a + jb;   = a – jb.

В этом случае

Если a>0, то имеют место колебания с частотой b и нарастающей амплитудой - движение неустойчиво.

Если a = 0, получим незатухающие колебания - система на грани устойчивости.

Если a<0, то амплитуда колебаний с течением времени уменьшается - колебания затухают.

Отсюда можно сделать следующие выводы:

- если все вещественные части корней характеристического уравнения отрицательны, то система устойчива (рис. 6.2);

- если хотя бы один из корней имеет положительную вещественную часть, то система неустойчива.

Если в каких-либо корнях характеристического уравнения вещественная часть равна нулю, а у остальных отрицательная, то об устойчивости невозмущенного движения по первому приближению ничего сказать нельзя и требуется специальное исследование полного уравнения.

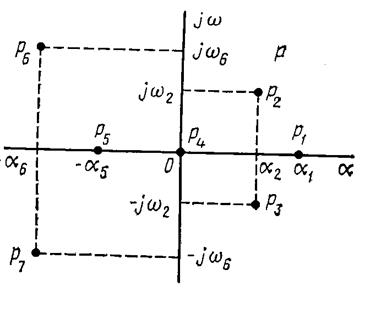
Рис. 6.2.

Если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то говорят, что система нейтрально устойчива. Этот случай называют критическим, и для определения устойчивости системы требуется специальное исследование нелинейных членов разложения.

6.3. Критерии устойчивости непрерывных САУ

Вычисление корней характеристических уравнений просто для уравнений 1-й и 2-й степеней. Если общие аналитические выражения для корней уравнений 3-й и 4-й степеней известны, но они громоздки и практически мало удобны. Уравнения более высоких степеней не имеют общих аналитических выражений для корней. Поэтому вычисление корней характеристических уравнений САУ следует выполнять на ЭВМ.

Кроме того, разработаны правила, которые позволяют определить устойчивость системы, минуя вычисление корней характеристического уравнения. Эти правила называют критериями устойчивости. Они позволяют в ряде случаев не только установить, устойчива ли система или нет, но и выяснить влияние тех или иных параметров и структурных изменений в системе на устойчивость.