Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 37

Подставим (2.3) в (2.1), рассматривая  как функцию независимых переменных , , , ,  и , разложим ее в ряд Тейлора в точке {, ,  , , } и отбросим малые члены ряда более высокого порядка, чем сами отклонения. Тогда уравнение (2.1) примет вид

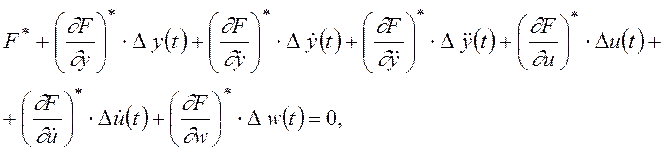
где звездочка сверху обозначает, что соответствующие функции и производные вычисляются в точке {, , , , , }.

Уравнение (2.1) выполняется во всех режимах, поэтому . В результате получим искомое линеаризованное уравнение звена в следующем виде:

Если время t не входит в явном виде в уравнение (2.1) и, кроме того, заданный режим является статическим (т. е. величины , , , , ,  не зависят от времени), то коэффициенты линеаризованного уравнения (2.4) являются постоянными величинами.

Уравнение (2.4) называют уравнением звена в отклонениях.

Уравнение (2.4) было получено при следующих предположениях:

1. Отклонения выходной () и входных ( и ) величин достаточно малы.

2. Функция  обладает непрерывными частными производными по всем своим аргументам в окрестности точки, соответствующей заданному режиму.

Если хотя бы одно из этих условий не выполняется, то линеаризацию проводить нельзя.

Для исследования устойчивости процессов управления такого приближения в большинстве случаев бывает достаточно. Однако при исследовании качества процесса управления указанные приращения переменных могут быть не всегда малыми. В этом случае для обеспечения требуемой точности в ряде Тейлора либо следует оставлять члены более высокого порядка малости, либо нужно применять нелинейное уравнение (2.1).

В результате линеаризации мы получили уравнение в отклонениях (или в приращениях), выраженное в абсолютных единицах. Каждый член уравнения имеет свою размерность. Однако при исследовании систем автоматического регулирования удобнее иметь уравнения в относительных единицах с безразмерными коэффициентами, имеющими размерность времени в степени, равной порядку производной, при которой стоит данный коэффициент.

При проведении дифференциального уравнения в абсолютных отклонениях к уравнению в относительных единицах с безразмерными коэффициентами следует произвести следующие элементарные операции.

1. Все члены уравнения делят на некоторую постоянную величину, имеющую размерность членов этого уравнения. Такой величиной может быть, например, номинальное значение, максимальное значение, некоторое начальное значение данной переменной. В результате этого каждый член уравнения станет безразмерным.

2. Переходят к относительным единицам. Выбирают постоянное значение для каждой координаты, каждого приращения, входящего в полученное уравнение, и к нему относят его приращение.

3. Вводят обозначения относительных единиц и коэффициентов уравнения.

В дальнейшем всегда, кроме специально оговариваемых случаев, будут применяться уравнения звеньев САУ в отклонениях. С целью упрощения записи сигналы и их отклонения будут обозначаться  одними и  теми  же  символами  (, , , и т. д.).

2.3. Математическое описание типовых законов управления

Устройства управления автоматических систем реализуют требуемые алгоритмы управления объектом. В САУ используют достаточно большое количество различных алгоритмов (законов) управления. Закон управления зависит от принципа действия, алгоритма функционирования, конструкции автоматической системы и от ее динамических свойств.

Алгоритмы управления, реализуемые оптимальными и адаптивными САУ, рассматриваются в соответствующих разделах настоящего учебного пособия. В данной главе ограничимся описанием наиболее распространенных (типовых) законов управления, реализуемых линейными регуляторами по отклонению непрерывного действия. С помощью таких простейших алгоритмов такие регуляторы формируют управляющее воздействие, линейно зависящее от сигнала рассогласования, его интеграла и первой производной по времени.

Типовые законы управления имеют следующее математическое описание:

1. Пропорциональный закон. С помощью этого алгоритма управляющее воздействие формируют пропорциональным сигналу рассогласования: