Так как звенья имеют различные передаточные функции, то они различаются по виду переходного процесса, который возникает при изменении входной величины. Для сравнения звеньев принято рассматривать переходный процесс при скачкообразном изменении входной величины на единицу и при нулевых начальных условиях (звено в покое), т.е. при единичном ступенчатом воздействии. Функцию, определяющую изменение величины на выходе звена при этих условиях, называют переходной функцией звена. Она может быть получена экспериментально путем записи изменения выходной величины при скачкообразном изменении входной. Эту функцию иногда называют кривой разгона. Частотные характеристики звеньев могут быть получены из дифференциальных уравнений (передаточных функций) звена, а также определяются экспериментально.
Можно указать следующие типовые звенья: апериодическое, колебательное, интегрирующее, усилительное, дифференцирующее и запаздывающее.
Структурной схемой в теории автоматического управления называют графическое изображение математической модели автоматической системы управления в виде соединений звеньев. Звено на структурной схеме условно обозначают в виде прямоугольника с указанием входных и выходных величин, а также передаточной функции внутри него. Иногда вместо передаточной функции указывают уравнение или характеристику. Звенья могут быть пронумерованы и их передаточные функции, уравнения или характеристики представлены вне структурной схемы.
Входные и выходные величины записывают в виде изображений, если передаточные функции задают в форме изображений. Если же передаточные функции задают в операторной форме или звенья описывают дифференциальными уравнениями, то входные и выходные переменные записывают в виде оригинала.
Сравнивающие и суммирующие (рис. 2.5) звенья изображают в виде круга, разделенного на секторы. В сравнивающем звене сектор, на который подается “вычитаемое”, затемняют (рис. 2.5, б) или перед соответствующим входом ставят знак минус (рис. 2.5, а).
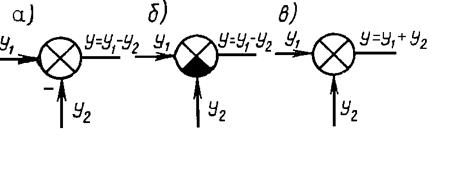
Рис. 2.5.
Структурную схему широко используют на практике при исследовании и проектировании автоматических систем управления, так как она дает наглядное представление о связях между звеньями, о прохождении и преобразовании сигналов в системе.
При математическом описании автоматическую систему обычно изображают в виде блок-схемы и для каждого “блока” (элемента) записывают уравнения, исходя из физических законов, которым подчиняются процессы в нем. Структурную схему можно составить на основании этой блок-схемы и полученных уравнений или только на основании последних. И дальнейшие преобразования, необходимые для получения уравнений и передаточных функций системы, проще и нагляднее производить по структурной схеме.
Звено на структурной схеме не обязательно изображает модель какого-либо отдельного элемента, соединения элементов или вообще другой части системы.
Основные правила преобразования структурных схем:
1.Последовательное
соединение звеньев (рис. 2.6, а). При последовательном соединении выходная
величина каждого предшествующего звена является входным воздействием
последующего. При преобразовании структурных схем цепочку из последовательно
соединенных звеньев можно заменить одним звеном (рис. 2.6, б) с передаточной
функцией W(s), равной произведению передаточных функций отдельных звеньев W(s) =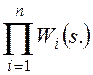
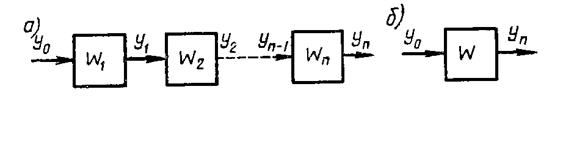
Рис. 2.6.
Запишем уравнение звеньев
y1 = W1×yo, y2 = W2×y1, ..., yn = Wn×yn-1.
Исключив из этой системы переменные y1, y2, ..., yn-1, получим
yn = W1×W2 ...Wn×yo,
откуда
W = yn/yo = 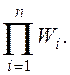
|
Рис. 2.7. |
Рис. 2.8. |
2. Параллельное
соединение звеньев (рис. 2.7). При параллельном соединении на вход всех
звеньев подается один и тот же сигнал, а выходные величины складываются. Цепь
из параллельно соединенных звеньев можно заменить одним звеном (рис. 2.7, б) с
передаточной функцией W(s), равной сумме передаточных функций входящих в нее
звеньев: W(s) = 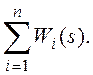
Для вывода этой формулы составим уравнения для каждого звена:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.