Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 66

Минимальный угол g, образуемый радиусом, проходящим через точку пересечения годографа  с окружностью единичного радиуса с центром в начале координат комплексной плоскости и отрицательной частью действительной оси, называют запасом устойчивости по фазе. Система обладает необходимым запасом устойчивости, если она, удовлетворяя условию устойчивости, имеет значение модуля характеристического вектора , отличающееся от единицы не менее чем на заданную величину h, называемую запасом устойчивости по модулю, и угол поворота или фазу, отличающуюся от (–p) не менее, чем на величину g, называемую запасом устойчивости по углу, или по фазе (рис. 6.5).

АФХ систем, обладающих требуемыми запасами устойчивости, не должны входить внутрь области I–I, II–II.

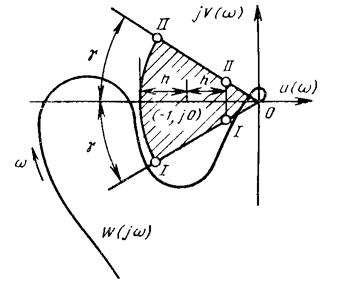
Рис. 6.5.

6.5. Анализ устойчивости дискретных САУ

Расположение полюсов дискретной передаточной функции на комплексной плоскости z. В примере 3.4.1 было показано, что дискретному звену с передаточной функцией

на входе которого нет экстраполятора, соответствует дискретная передаточная функция

с полюсом в точке

Разностное уравнение, описывающее эту систему, имеет вид

Полагая, что сигнал на входе системы отсутствует, т. е. u(k) = 0, k ³ 0, и начальное значение выхода равно y(0) ¹0, приходим к однородному разностному уравнению

Отсюда можно получить следующую последовательность выходных сигналов:

Переходный процесс в системе сходится к нулю, а сама система, следовательно, асимптотически устойчива только при условии ½a₁½<1. Вид переходных процессов для различных положений полюса a₁ на плоскости z иллюстрируется рисунке 6.6. Заметим, что при отрицательных значениях a₁ наблюдаются колебания.

Полюса передаточных функций системы по sи по z связаны соотношением

Отсюда следует, что полюсам на плоскости s, расположенным в области , на плоскости z соответствуют полюса ¥> z₁>0. Таким образом, на плоскости s отсутствует действительный полюс, соответствующий отрицательному значению z₁.

Комплексно-сопряженные полюса. Система второго порядка с передаточной функцией

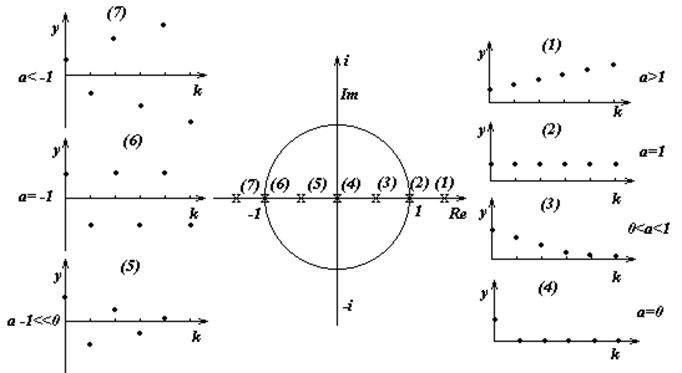
Рис. 6.6.

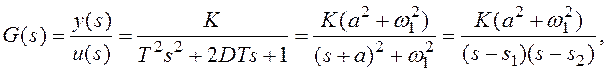
где a = D/T, w²₁ = 1/T²(1 - D²), s_1,2 = - a ± iw₁ без эктраполятора нулевого порядка при входе обладает дискретной передаточной функцией

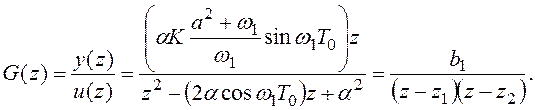
Здесь

Полюса этой дискретной передаточной функции равны

а соответствующее ей разностное уравнение имеет вид

y(k) - (2a cos w₁T₀) y (k -1) + a²y (k -2) = 0.

Запишем решение этого уравнения при начальных условиях

y(0)=0 , y(1) = a cos w₁T₀

в следующем виде:

y(k) = a^k cos w₁kT₀y(0).

Графики изменения y(k) для положительных значенийa изображены на рисунке 6.7 (граничная частота w_Sh = p/T₀). При отрицательных a переходные процессы носят колебательный характер. Следует, однако, иметь в виду, что на плоскости s соответствующие этим значениям полюса не существуют.

Условие асимптотической устойчивости. Линейная система именуется асимптотически устойчивой, если после конечного однократного воздействия она возвращается к своему положению равновесия. Проведенный выше анализ влияния расположения полюсов на переходные процессы показал, что данное условие соблюдается только в том случае, когда полюса находятся внутри единичного круга на плоскости z.

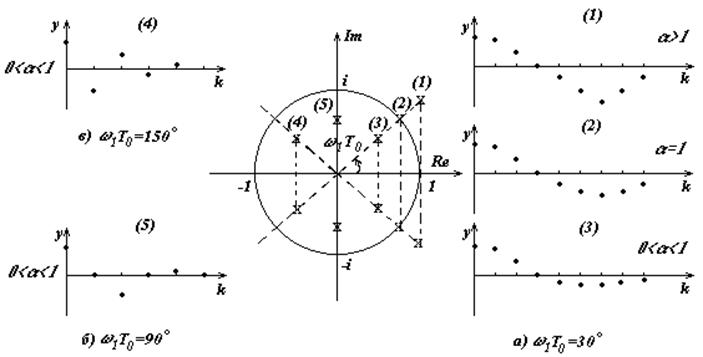
Рис. 6.7.

Иными словами, корни характеристического уравнения

(z - z₁)(z - z₂) ... (z - z_m) = 0

должны удовлетворять неравенству

|z_i|<1,  i = 1, 2, ..., m.

Билинейное преобразование и критерии устойчивости. Билинейное преобразование

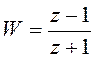
переводит точки единичной окружности на  плоскости z в  точки, лежащие на мнимой оси плоскости w. Поскольку плоскость w в теории дискретных систем служит аналогом плоскости s для непрерывных систем, в ней можно применять критерии устойчивости Рауса или Гурвица.