|
№ варианта |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
q |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
A1,1 |
-0.1 |
-0.2 |
-0.3 |
-0.4 |
-0.5 |
-0.6 |
-0.7 |
-0.8 |
-0.9 |
-1.0 |
-0.1 |
-0.2 |
-0.3 |
-0.4 |
|
A1,2 |
-0.1 |
-0.2 |
-0.3 |
-0.4 |
-0.5 |
-0.6 |
-0.7 |
-0.8 |
-0.9 |
-1.0 |
-1.1 |
-1.2 |
-1.3 |
-1.4 |
|
A2,1 |
0.5 |
1.0 |
1.5 |
2.0 |
1.5 |
1.0 |
0.5 |
1.0 |
1.5 |
2.0 |
1.5 |
1.0 |
0.5 |
1.0 |
|
b |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
0.7 |
1.8 |
1.9 |
1.0 |
1.0 |
0.75 |
1.20 |
1.35 |
|
|
0.5 |
-0.5 |
0.6 |
-0.6 |
0.5 |
-0.5 |
0.4 |
-0.4 |
0.3 |
-0.3 |
0.4 |
-0.4 |
0.5 |
-0.5 |
При выполнении лабораторной работы необходимо:
6. Выполнить анализ управляемости и наблюдаемости объекта управления.
7. Составить математическую модель системы управления в пространстве состояний.
8. Составить функционал МНК для задачи идентификации параметров ПИ-регулятора и определить оценки параметров ПИ-регулятора.
9.
Моделированием на ЭВМ определить
графики переходных процессов для управляемой переменной ![]() и
управляющего воздействия
и
управляющего воздействия ![]() . Шаг квантования времени
принять равным
. Шаг квантования времени
принять равным ![]() =0,01 с.,
=0,01 с., ![]() =0,
1, …, N. Требуемый закон изменения выходного сигнала
измерительного устройства задан формулой:
=0,
1, …, N. Требуемый закон изменения выходного сигнала
измерительного устройства задан формулой:
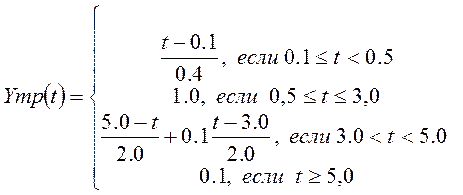 (4)
(4)
возмущающее воздействие формируется окружающей средой следующим образом:
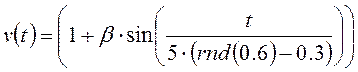 .
.
По графикам переходных процессов определить прямые показатели качества регулирования.
10. Составить отчет по лабораторной работе.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
Система управления (рис. 1) имеет следующую модель:
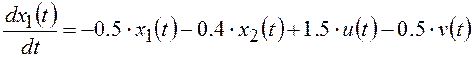 ; (a)
; (a)
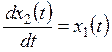 .
(b)
.
(b)
3. Составление модели системы управления в пространстве состояний
Из рисунка 2 видно, что в пространстве состояний регулятор можно описать уравнениями:
![]() ;
(6)
;
(6)
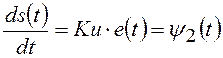 ,
(7)
,
(7)
где невязка (величина сигнала рассогласования) ![]() определяется по формуле:
определяется по формуле:
![]() ;
(8)
;
(8)
![]() - вспомогательная переменная состояния
регулятора.
- вспомогательная переменная состояния
регулятора.
Из формул (2)-(8) видно, что система, образованная регулятором, объектом управления и измерительным устройством, имеет следующую математическую модель в пространстве состояний:
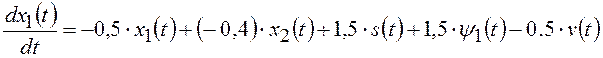 ;
;
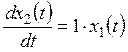 ;
;
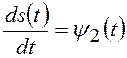 ;
;
![]() .
.
Эту систему уравнений запишем в матричном виде:
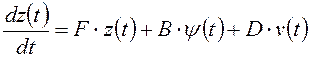 ;
(I)
;
(I)
![]() ,
(II)
,
(II)
где:
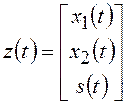 ;
; 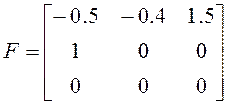 ;
; 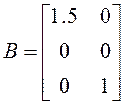 ;
; 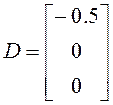 ;
; ![]() .
.
Таким образом, получена модель САУ в пространстве состояний в виде системы уравнений (I), (II) и (8).
2. Определение параметров ПИ-регулятора
Параметры ПИ-регулятора будут определены минимизацией функционала обобщенной работы
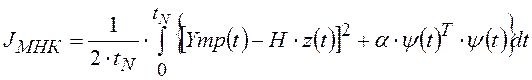
по переменной ![]() с
учетом ограничений, заданных уравнениями (I), (II), (III) и (8), где
с
учетом ограничений, заданных уравнениями (I), (II), (III) и (8), где ![]() -
весовой коэффициент.
-
весовой коэффициент.
Минимизация этого
функционала по переменным ![]() и
и ![]() с учетом ограничений (I), (II) и (8) с помощью принципа максимума приводит к следующим
уравнениям для оптимальных траекторий
с учетом ограничений (I), (II) и (8) с помощью принципа максимума приводит к следующим
уравнениям для оптимальных траекторий ![]() вектора
переменных состояния
вектора
переменных состояния ![]() :
:
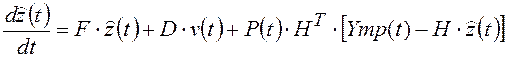 ;
(3.1)
;
(3.1)
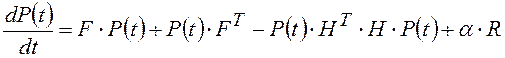 ,
(3.2)
,
(3.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.