Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 57

где D - постоянная величина, значение которой нужно оговаривать. Задается величина D в процентах от установившегося значения выходной величины _.

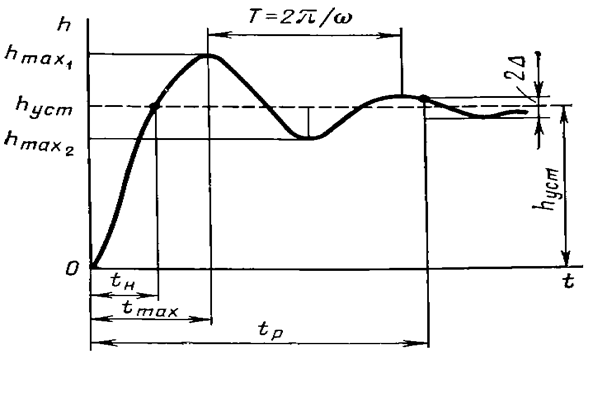
Рис. 5.1.

2. Перерегулирование s- максимальное отклонение переходной характеристики от установившегося значения выходной величины, выраженное в процентах:

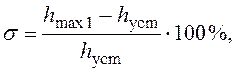
где  - значение первого максимума.

Допустимое значение перерегулирования в каждом конкретном случае будет подсказано опытом эксплуатации системы. Обычо s = 10 ÷ 30%, но в некоторых случаях допускается и до 70%. Иногда перерегулирование недопустимо совсем.

3. Частоту колебаний w = 2p/Т, где Т - период колебаний для колебательных переходных характеристик.

4. Число колебаний n, которое имеет переходная характеристика h(t) за время регулирования t_p.

При проектировании систем чаще всего допускают n = 1 ÷ 2, а иногда и до 3 ÷ 4, но в некоторых случаях колебания в системе недопустимы.

5. Время достижения первого максимума t_max.

6. Время нарастания переходного процесса t_н - абсцисса первой точки пересечения кривой переходной характеристики h(t) с уровнем установившегося значения h_уст.

7. Декремент затухания c, равный отношению модулей двух смежных перерегулирований:

c = çh_maxl - h_устê/ç h_max2 - h_уст ç.

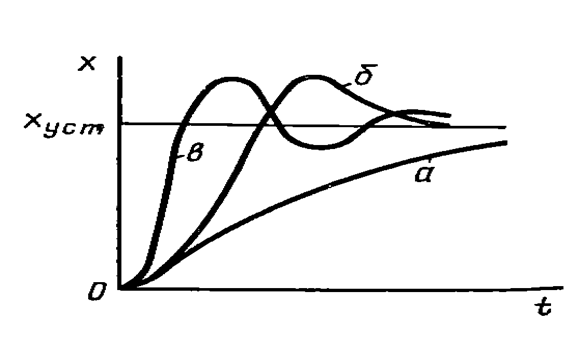
Рис. 5.2.

Нужно отметить, что в настоящее время при существующем развитии вычислительной техники трудности, связанные с расчетом переходных процессов и выбором возможных вариаций параметров системы, существенно уменьшаются, поэтому роль прямых оценок качества при проектировании систем автоматического управления возрастает.

В качестве примера может быть рассмотрена следящая система для управления антенной радиолокационной станции. На входной сигнал такой системы, который воспроизводит действительный закон движения цели, накладываются помехи, или флюктуации, представляющие собой быстро изменяющиеся случайные функции времени. Флюктуации входного сигнала создаются непрерывным изменением коэффициента отражения самолета вследствие "рыскания" и качки последней, а также неоднородности отражающей поверхности и других причин. Такого рода воздействия при анализе систем не могут быть заменены типовыми воздействиями в виде заданной функции времени, и в то же время ими нельзя пренебречь, так как от них зависит общая величина ошибки системы. При этом такие показатели качества, как статическое отклонение регулируемой величины, число колебаний, перерегулирование, теряют смысл. Сохраняет значение или максимальное отклонение x_max регулируемой величины или среднее ее значение х за достаточно большой промежуток времени.

5.2. Интегральные критерии качества управления

Интегральные критерии качества являются интегралами по времени от некоторых функций переходного процесса погрешности управления . Цель использования таких критериев состоит в том, чтобы получить общую оценку быстродействия и отклонения управляемой величины от установившегося значения, применяя для этого линейные и квадратические интегральные критерии.

Линейные критерии качества управления. Чаще используют моменты i-го порядка, т. е. критерии вида

Простейшим из них является критерий J_oo. Если система устойчива, то , интеграл J_oo  стремится к конечному значению, равному площади под кривой  (рис. 5.3). Чем выше быстродействие системы, тем меньше величина J_oo, поэтому параметры системы следует выбирать так, чтобы величина критерия J_oo стремилась к минимуму, т. е. dJ_oo/da = 0  где a - варьируемый параметр системы. Недостатком этого критерия является то, что он применим к монотонным или апериодическим процессам. При колебательном переходном процессе (рис. 5.4) площади, ограниченные кривой , складываются алгебраически и минимуму J_oo может соответствовать процесс с большим числом колебаний n, т. е. с малым быстродействием и даже с незатухающими колебаниями.

Рис. 5.3.                                                         Рис. 5.4.