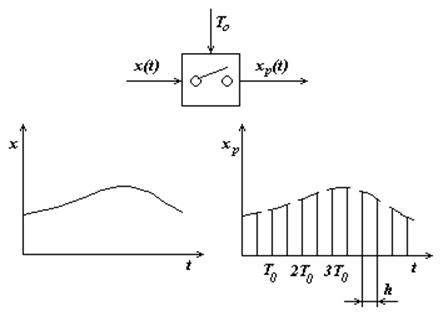
Рис. 3.5.
Для получения разностного уравнения достаточно любую дискретную функцию, зависящую от другой дискретной функции, представить в рекуррентной форме. Линейное разностное уравнение порядка m имеет вид
|
x(k) + a1x(k – 1) + ... + amx(k – m) = b0w(k) + b1w(k – 1) + ... + bmw(k – m). |
(3.1) |
Здесь аргумент k×T0 заменен индексом k.
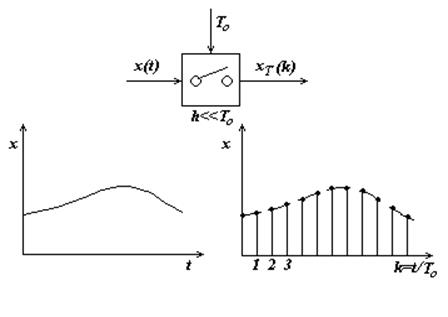
Рис. 3.6.
Величину выходного сигнала при любом k можно вычислить с помощью рекуррентной формулы
|
x(k) = – a1x(k – 1) – ... – amx(k – m) + b0w(k) + b1w(k – 1) + ... + bmw(k – m), |
(3.2) |
если известны текущее значение входа w(k) и m предшествующих значений w(k – 1), ...., w(k – m), а также соответствующие значения выхода x(k – 1), ..., x(k – m).
Другой способ построения разностных уравнений состоит в дискретизации дифференциальных уравнений. При этом дифференциальное уравнение первого порядка аппроксимируют разностным уравнением первого порядка, дифференциальное уравнение второго порядка – разностным уравнением второго порядка и т. д. При замене дифференциалов левыми разностями справедливы следующие соотношения, приведенные в таблице 3.1.
В примерах раздела 3.6 показано, как осуществляется дискретизация некоторых дифференциальных уравнений.
Выражение (3.1) является наиболее распространенной формой записи разностных уравнений. Если использовать разности высших порядков вплоть до m-го, разностное уравнение можно представить в виде
|
amDmx(k) + am-1Dm-1x(k) + ... +a1Dx(k) + x(k) = = bmDmw(k) + bm-1Dm-1w(k) + ... + b1Dw(k) + b0w(k), |
(3.3) |
которое эквивалентно дифференциальному уравнению m-гопорядка.
Таблица 3.1
|
Непрерывная функция |
Дискретная функция |
|
первая производная |
разность первого порядка |
|
|
|
|
вторая производная |
разность второго порядка |
|
|
|
Описанные способы аппроксимации дают удовлетворительные результаты только в тех случаях, когда такт квантования T0 мал по сравнению с постоянной времени T.
Эффективный математический метод описания дискретных функций основывается на замене последовательности импульсов xp(t) решетчатой функцией, состоящей из идеальных импульсов. Идеальный импульс определяется как дельта-функция Дирака:
|
|
(3.4) |
а его площадь равна
|
|
(3.5) |
Если продолжительность замыкания ключа значительно меньше такта квантования, т. е. h £ T0, импульсы последовательности xp(t), имеющие площадь x(t)×h, можно приближенно заменить идеальным импульсами d(t) той же площади, то
|
|
(3.6) |
Решетчатая функция xd(t) физически нереализуема: она служит лишь удобной формой представления последовательности реальных импульсов xp(t). Введение идеального квантователя, формирующего d-импульсы, позволяет значительно упростить прохождение дискретных сигналов через линейные динамические звенья. Этот приближенный переход иллюстрируется на рисунке 3.7. Предполагается, что площади реальных и соответствующих им идеальных импульсов одинаковы.
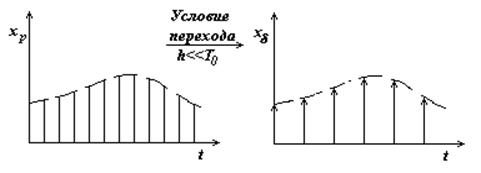
Рис. 3.7.
Учитывая, что последовательность идеальных импульсов определена лишь в моменты времени t = k×T0, k = 0, 1, 2, ..., уравнение (3.6) можно переписать в виде
|
|
(3.7) |
При анализе динамических систем с одинаковыми, синхронно работающими ключами на входе и выходе, продолжительность замыкания h не учитывается. Фактически эта величина не влияет на конечный результат, если за ключом стоит экстраполятор. Поэтому ее можно выбрать произвольно, например положить для простоты h = 1 с. В этом случае последовательность идеальных импульсов описывается выражением
|
|
(3.8) |
В выражении (3.8), полученном после нормализации (3.7), выходные сигналы квантователя (рис. 3.5) умножаются на идеальные импульсы d(t - kT0).
Преобразование Лапласа. Применим к идеальному импульсу преобразование Лапласа:
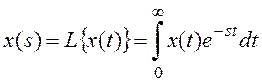 ,
,
где s = s + iw- комплексная переменная. В результате получим
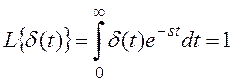 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.