Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 75

*  параллельное оценивание неизвестных ковариационных матриц;

*  исследование проблем нелинейной фильтрации: одновременное получение оценок состояния и параметров объекта; оценивание состояния нелинейных объектов.

7.7. Примеры и задачи

Пример 7.1. Рассмотрим объект второго порядка с передаточной функцией

G_p (z) =

a). Каноническая форма управляемости:

A =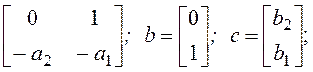

A(z) = det [zI - A] = Az² + a₁z + a₂;

B(z) = [b₂b₁]×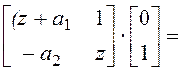

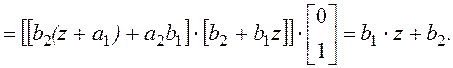
В случае диагональной матрицы F имеем

.

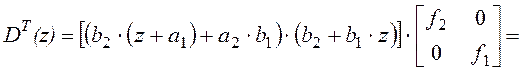
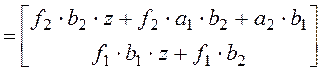Если входной сигнал x_i(k) представляет собой белый шум, коэффициенты полиномов числителей в уравнении (7.51) D_i(z) = d_1i×z +d_2i можно определить, задаваясь следующими условиями:

x_i(k) ¹0; x₂(k) = 0; f₁¹0; f₂ ¹0;

d_1i = f1×b1;

d_2i = f1×b2.

x_i(k) =0; x₂(k) ¹0; f₁ =0; f₂ ¹0;

d₁₂ = f₂×b_2;

d₂₂ = f₂×a₁×b₂ + a₂×b₁.

Таким образом, параметры d_1i и d_2iне могут принимать произвольные значения, поскольку они зависят друг от друга, и выбор одного коэффициента однозначно определяет величину другого.

б). Каноническая форма наблюдаемости:

А =

A(z) = z² +a₁×z+a₂;

B(z) = [0  1]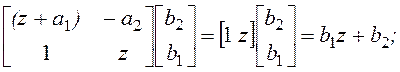

D^T(z) = [1  z]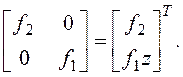

Следовательно, для данной формы описания числители фильтров помехи имеют вид

D₁(z) = d₂₁z = f₁z  при x₁(k) ¹0; x₂(k) = 0;

D₂(z) = d₁₂ =  f₂  приx₁(k) = 0;  x₂(k) ¹0.

Вновь коэффициенты d_1i и d_2i нельзя задавать произвольно, так как один из этих параметров всегда должен быть равен нулю.

Приведенный пример позволяет заключить, что в тех случаях, когда сигнал возмущения x(k) или v(k) является векторным "белым шумом" с независимыми случайными компонентами, параметры числителей соответствующих формирующих фильтров могут принимать лишь вполне определенные значения. Однако, данное правило не действует, если, например, все составляющие случайного возмущения равны между собой:

x₁(k) = x₂(k) = . . . = x_m(k) = x(k).

При этом матрица F преобразуется в вектор

f^т = [f_m  f_m-1 . . . f₁].

Числитель формирующего фильтра в примере 7.1. принимает вид

D(z) = d₁×z + d₂,

причем:

а) для канонической формы управляемости

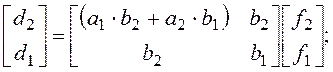
б) для канонической формы наблюдаемости

d₂ = f₂,

d₁ = f_1.

 Очевидно, параметры полинома D не зависят друг от друга, а все элементы ковариационной матрицы возмущения имеют одинаковые значения, т. е.

Поскольку при s_x ¹ 0 эта матрица положительно полуопределена, по-прежнему справедлива модель (7.21).

Пример 7.2. Рассмотрим скалярную систему

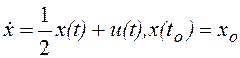
и функцию стоимости

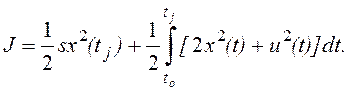
Поэтому, решение можно записать либо как

либо

где x₁ иx₂ выбраны так, чтобы p(t_j) = s.

Например, если

а) s = 0, t_j = 1, то x₁ = 1,845 радиан, что дает

K(t) = -R^-1 B^T P= 0,5 - 1,5 th( - 1,5t + 1,845).

Поскольку s = 0, то мы не придаем особого значения состоянию в конечный момент времени и “усиление” (и управление) в конечный момент времени стремится к нулю;

б) s = 10, t_j = 10, тогда  x₂ = 15,1425 радиан. В этом случае ошибке при t = t_j придается большой вес, и в момент достижения усиление становится большим (-10);

в) s = ¥, непосредственного решения уравнения Риккати получено быть не может, так как начальное условие бесконечно. Можно решить “инверсное” уравнение Риккати при нулевом граничном условии, в результате чего получим

Легко показать, что если t_f не ограничено, то K(t) становится равным единице и, как следовало ожидать, усиление обратной связи становится постоянным.

Пример 7.3.  В данном примере будет рассмотрена простая скалярная задача, которая решается достаточно просто. Минимизируется функция стоимости

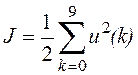
при ограничении  в форме равенств

x(k+1) = x(k) + a× u(k),       x(o) = 1,

x(10) = 0.

Вводя заданное ограничение в исходную функцию стоимости с помощью множителей Лагранжа, получим

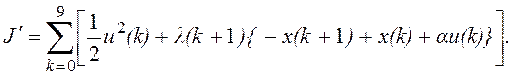
Множители Лагранжа введены потому, что это приводит к упрощению конечного результата. Для рассматриваемого примера

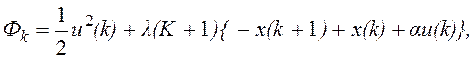
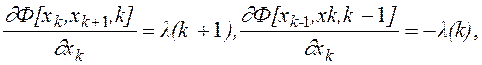
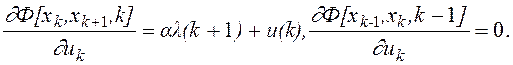
Таким образом, дискретное уравнение Эйлера - Лагранжа (7.18) имеет вид

l(k) - l(k+1) = u(k)+a×l(k+1) = 0.

Кроме того, исходное уравнение должно быть справедливо при заданных граничных условиях

x(k+1) = x(k)+a× u(k),       x(0) = 1,      x(10) = 0.