Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 41

Анализ влияния возмущений на САУ в пространстве состояний. Возмущения можно рассматривать как выход линейных динамических систем, поэтому можно непосредственно проанализировать их воздействие на САУ. Обычно (как это указывалось) возмущения можно считать решениями линейных дифференциальных уравнений с некоторыми начальными условиями (задачи Коши), поэтому нетрудно исследовать их влияние на линейные системы. К переменным состояния просто добавляются переменные, описывающие возмущения. Система уравнений затем решается с начальными условиями, которые должны соответствовать этим возмущениям.

2.7. Передаточная функция и частотные характеристики

Передаточные функции. При описании автоматических систем управления широко используют символическую форму записи линейных дифференциальных уравнений в форме передаточных функций.

Передаточной функцией (или передаточной функцией в форме изображений Лапласа) называют отношение изображения Лапласа выходного сигнала к изображению Лапласа входного сигнала, вычисленных при нулевых начальных условиях.

Если звено (система) имеет несколько входов, то при определении передаточной функции относительно какой-либо одной входной величины остальные входные величины полагают равными нулю.

Рассмотрим получение передаточных функций на примере звена, математическую модель которого описывают уравнением (2.12):

Звено, описываемое уравнением (2.12), можно характеризовать двумя передаточными функциями: передаточной функцией по входному сигналу u и передаточной функцией по входному сигналу f.

Перейдем в обеих частях этого уравнения к изображениям Лапласа:

Используя свойства преобразования Лапласа (линейности и дифференцирования оригинала), вычисленного при нулевых начальных условиях, получим

где Y(s) = L{y(t)},  U(s) = L{u(t)},  F(s) = L{f(t)}.

Полагая последовательно F(s) = 0  иU(s) = 0 и определяя каждый раз отношение выходного сигнала к входному, получим

Передаточные функции  и  можно получить из дифференциального уравнения, если в последнем сделать подстановку 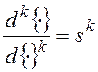. В общем случае это следует из того, что оператору дифференцирования функции-оригинала преобразования Лапласа при нулевых начальных условиях соответствует умножение функции-изображения Лапласа на комплексную переменную s.

Используя передаточные функции (2.20), уравнение (2.12) можно записать в изображениях Лапласа:

Это уравнение, как и уравнение (2.19), адекватно исходному дифференциальному уравнению (2.12) только при нулевых начальных условиях. Если начальные условия не равны нулю, то уравнениями (2.19) и (2.21) как математическими описаниями исходного звена пользоваться нельзя.

Частотные характеристики. Важную роль при описании линейных стационарных систем (звеньев) играют частотные характеристики. Их получают при рассмотрении вынужденных движений системы (звена) при подаче на ее вход гармонического воздействия.

Для линейных систем справедлив принцип суперпозиции, который можно сформулировать следующим образом:  реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности.

Это позволяет ограничиться изучением систем с одним входом. В общем случае линейная стационарная САУ с одним входом имеет следующую математическую модель:

Ее передаточная функция по определению равна

Функцию , которую получают из передаточной функции (2.23) при подстановке в нее :

называют частотной передаточной функцией. Частотная передаточная функция является комплексной функцией  действительной переменной w, которая называется частотой.

Функцию можно представить в виде

где