Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 56

m(k) ®0,

P(k) ®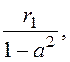

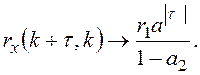
В этом случае процесс становится стационарным, так как m есть константа, а ковариация зависит только от t.

Если ввести вход y(k) = x(k) + e(k), где е - последовательность некоррелированных случайных величин с нулевым математическим ожиданием и ковариацией r₂, то ковариация y принимает следующий вид:

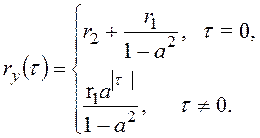
Спектральную плотность вычисляют по уравнению

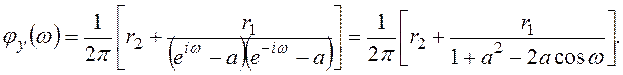
Задача. 4.1.Используйте теорему 4.1 для вычисления стационарной ковариации процесса

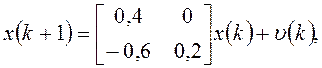
где v – "белый шум" с нулевым математическим ожиданием и ковариацией

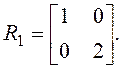
Задача. 4.2.Имеется стационарный стохастический процесс, генерируемый системой

x(k + 1) = Ф х(k) + v(k)

y(k) = C x(k),

где v(k) - последовательность одинаково распределенных случайных переменных с нулевым математическим ожиданием. Пусть характеристическое уравнение матрицы А имеет вид

zⁿ + a₁z^n-1 + ... + a_n = 0.

Покажите, что автоковариация выхода r_y(t) удовлетворяет уравнению

r_y (t) + a₁r_y (t - 1) + ... + a_nr_y (t - n) = 0

для t³ n + 1.

Задача. 4.3.Имеется процесс

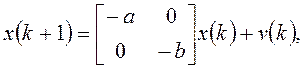
y(k) = [1   1] x(k),

где v(k) – "белый шум" с нулевым математическим ожиданием и ковариацией

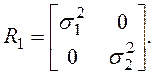
Покажите, что y(k) можно представить в виде

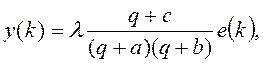
где e(k) – "белый шум" с нулевым математическим ожиданием и единичной дисперсией. Найдите уравнение, из которого можно определить l и с.

Задача. 4.4.Стохастический процесс y(k) описывается уравнениями

x(k + 1) = a x(k) + v(k),

y(k) = x(k) + e(k),

где v и е - нормально распределенные процессы типа "белого шума" со следующими свойствами:

M{v(k)} = M{e(k)} = 0;

M{v(k)²} = 1;

M{e(k)²} = r₂;

M{v(k) e(k)} = r₁₂ при k = j и 0 в противном случае.

Покажите, что y(k) можно представить как выход линейного фильтра

y(k) =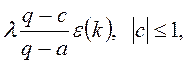

где e(k) – "белый шум" с нулевым математическим ожиданием и единичной дисперсией. Определите l и с.

Задача. 4.5.Найдите ковариацию r_y(t) и спектральную плотность j_y(w) процесса y(k), если

y(k) - 0,7 y(k - 1) = e(k) - 0,5 e(k -1),

где e(k) – "белый шум" с единичной дисперсией.

Задача. 4.6.Определите дисперсию стохастического процесса y(k), заданного уравнением

y(k) - 1,5 y(k - 1) + 0,7 y(k - 2) = e(k) + 0,2 e(k - 1),

где е– "белый шум" с единичной дисперсией.

Γлава 5. АНАЛИЗ КАЧЕСТВА ПЕРЕХОДНЫХ ПРОЦЕССОВ В САУ

Любое воздействие вызывает в системе переходный процесс, по окончании которого система переходит в новое установившееся состояние. Поэтому при исследовании систем автоматического управления приходится решать задачу обеспечения требуемых показателей качества переходного процесса. Показатели качества, определяемые непосредственно по кривой переходного процесса, называют прямыми оценками качества. Кривая переходного процесса может быть получена теоретически или экспериментально. Но часто возникают существенные трудности, так как расчет переходного процесса в системах высокого порядка сложен, а эксперимент не всегда осуществим. Поэтому используют косвенные методы оценки качества, полученные иным путем, не требующим нахождения кривой переходного процесса.

Существующие прямые и косвенные методы оценки качества управления подробно описаны в литературе. Поэтому в данной главе будут рассмотрены только некоторые из них.

5.1. Прямые оценки качества переходного процесса при внешнем воздействии

в виде ступенчатой функции

Переходный процесс в системе является ее реакцией на внешнее воздействие, которое в общем случае может быть сложной функцией времени. Обычно рассматривают поведение системы при следующих типовых воздействиях: единичной ступенчатой функцией 1(t), импульсной d(t) и гармонической функциями. Чаще всего прямые оценки качества получают по кривой переходной характеристики h(t), т. е. по выходному сигналу системы при воздействии единичной ступенчатой функции

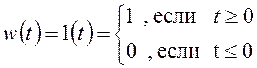
и нулевых начальных условиях.

К прямым оценкам качества относят (рис. 5.1):

1. Время регулирования  t_P - минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью: