Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 76

Из последних двух уравнений получим

l(k) = const = c,      u(k) = -a× c,    x(k+1) = x(k) - a²× c.

Это окончательное разностное уравнение, которое надо решить. Получим

x(1) = x(0) - a²×c,

x(2) = x(1) - a²× c = x(0) - 2 a²×c,

x(3) = x(2) - a²×c = x(0) - 3 a² ×c,

…………………………….

x(k) = x(0) - k×a²×c.

Для выполнения граничных условий необходимо

x(10) = 0 = x(0) - 10a² ×c,          c =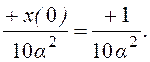

Следовательно, управление, которое следует приложить к дискретной системе, u(k)=-1/10a. Результирующая траектория - x(k) = 1 - k/10.

Глава 8. АДАПТИВНОЕ УПРАВЛЕНИЕ

8.1. Самонастраивающиеся регуляторы

Для реализации методов, описанных в предыдущих главах, требуется последовательно пройти все этапы процесса: моделирование, идентификацию, проектирование системы управления и анализ чувствительности. Не исключено, что эти стадии, может быть, придется пройти не один раз, чтобы получить приемлемые результаты. Возникает вопрос: а нельзя ли упростить столь длительную итерационную процедуру путем введения более сложных регуляторов, автоматизации самой процедуры конструирования? Оказывается, можно, если включить в регулятор алгоритмы оценки параметров и конструирования управления. Такой подход приводит к понятию так называемых самонастраивающихся регуляторов (СНР). Хотя подобные регуляторы имеют существенно более сложную структуру, чем регуляторы с постоянным усилением, их довольно просто реализовать на практике с помощью программируемых микропроцессоров.

Замкнутые системы, включающие самонастраивающиеся регуляторы, почти всегда являются нелинейными и нестационарными, и для их анализа требуются иные подходы, принципиально отличающиеся от подходов, описанных ранее в данном пособии.

Небольшие модификации самонастраивающихся регуляторов позволяют получить адаптивные регуляторы, способные работать в системах с широким диапазоном изменения регулируемых параметров.

Один из способов автоматизации моделирования и конструирования системы управления можно схематично представить в виде следующей последовательности операций: выбор подходящей структуры модели и оценка значения ее параметров с помощью рекурсивных методов, описанных в главе 7; построение закона управления по полученным оценкам каким-либо методом из описанных в главах 2-7. Блок-схема такой системы показана на рисунке 8.1. Построенный таким образом регулятор является самонастраивающимся, поскольку у него есть механизм настройки его собственных параметров и его можно рассматривать как двухконтурную систему. Внутренний контур включает сам процесс и обычный линейный регулятор со звеном обратной связи; внешний контур включает блоки рекурсивной оценки параметров и расчета законов управления и предназначен как раз для настройки регулятора.

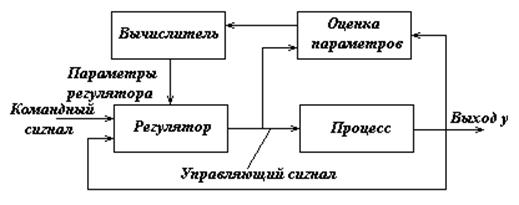
Рис. 8.1.

Блок расчета управления (рис.8.1) в реальном масштабе времени решает задачу аналитического конструирования регулятора для системы с известными параметрами.

Самонастраивающийся регулятор обладает большой гибкостью по отношению к выбору метода конструирования. В нем можно использовать практически любой из известных методов конструирования, а также различные схемы оценки параметров, описанные в литературе по адаптивным САУ, - стохастическую аппроксимацию, метод наименьших квадратов (МНК), метод максимума правдоподобия, фильтр Калмана и др.

Самонастраивающиеся регуляторы делятся на два класса: явные и неявные. В явных алгоритмах производится оценка параметров явной модели процесса. Вместе с тем иногда можно выразить модель процесса через параметры самого регулятора. В этом случае алгоритм существенно упрощается, поскольку отпадает необходимость расчета управлений. Такой регулятор называют неявным, так как он основан на оценке неявной модели процесса.

8.2. Задача управления

Рассмотрим задачу конструирования методом размещения полюсов передаточной функции. Пусть процесс описывается следующей моделью без учета возмущений:

где:

 u - управляющий сигнал,