Экстремальные системы поддерживают экстремальное (максимальное или минимальное) значение некоторого показателя качества или эффективности функционирования объекта автоматизации. Показатель качества при этом выражается функцией текущих координат автоматической системы.
На рисунке 1.7 показана функциональная схема экстремальной системы управления. Система измерительных преобразователей (ИП) собирает и передает информацию об изменениях выходных переменных у(t) объекта управления (ОУ) в процессе функционирования системы в вычислительное устройство (ВУ), которое определяет показатель качества J(у(t)). Устройство пробных воздействий (УПВ) генерирует управляющие пробные воздействия, которые передаются на систему управляющих органов (УО) объекта (ОУ) через преобразующие элементы (ПЭ). Логическое устройство (ЛУ), получая информацию о введенных пробных воздействиях и об изменениях под их влиянием показателя J(у(t)), анализирует полученные данные и результат передает устройству формирования команд управления (УФКУ).
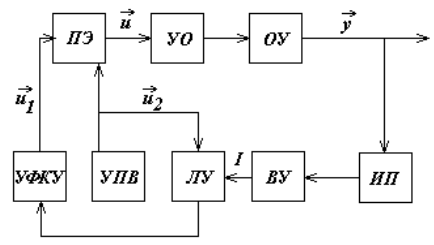
Рис. 1.7.
Сформированные команды управления после их преобразования и усиления в системе преобразующих элементов (ПЭ) поступают на управляющие органы (УО) объектов управления и обеспечивают такой алгоритм функционирования автоматической системы, при котором достигается экстремум показателя качества. Совокупность функциональных и логических элементов ВУ, ЛУ, УФКУ по существу представляет собой счетно-решающее устройство, в качестве которого обычно используется микропроцессор или микроЭВМ.
Одной из важнейших операций алгоритма экстремального управления является поиск экстремума показателя качества. Так как значение показателя качества регулярно отклоняется от экстремального в результате внешних воздействий на объект управления, его необходимо постоянно контролировать. Для этого периодически на управляющие органы (УО) подают небольшие пробные воздействия и анализируют реакцию системы на них, а затем осуществляют соответствующее управление. Если функция J(у(t)) многоэкстремальна, то возникает необходимость поиска всех локальных экстремумов и выявления глобального экстремума. Для этого приходится просматривать всю рабочую область. Положение осложняется еще и тем, что объект может иметь несколько управляющих органов, что значительно увеличивает число пробных воздействий. В результате пробных воздействий процесс функционирования отклоняется от оптимального и показатель качества снижается, что обусловливает так называемые потери на поиск. Особенно значительны потери в начальный период работы автоматической системы, пока она выходит на режим.
Поскольку в системах экстремального управления измеряется значение управляемой переменной, то при их реализации используется фундаментальный принцип управления по отклонению.
Для систем, в которых пробные воздействия могут нарушить нормальное функционирование и значительно ухудшить их технико-экономические показатели, экстремальное управление неприемлемо. В таких случая применяют методы оптимального управления.
Системы оптимального управления.В конце 50-х годов Р. Беллман и Л. С. Понтрягин показали, что многие задачи управления могут быть сформулированы как задачи оптимизации. Для нелинейных систем это привело к неклассическому вариационному исчислению. Р. Беллманом было найдено точное решение для линейных систем с квадратичными функциями потерь. В своей знаменитой работе Р. Калман доказал, что линейная квадратичная задача сводится к решению дифференциального уравнения Риккати. Он также показал, что классическая задача фильтрации случайных возмущений (Н. Винера) может быть переформулирована в рамках теории пространства состояний. Это позволило добиться "решения" с помощью рекурсивных уравнений, очень удобных для решения на ЭВМ.
В начале 60-х годов стохастическая вариационная задача была сформулирована исходя из предположения, что возмущения являются случайными процессами. Задачу оптимального управления для линейных систем смогли сформулировать и решить для случая квадратичных потерь. Это привело к развитию теории стохастического управления. В результате возникла теория оптимального управления системами с квадратичным критерием качества, которая сейчас является основным средством проектирования многомерных линейных систем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.