Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 11

Дискретный "белый шум".Рассмотрим стационарный дискретный стохастический процесс , такой, что его реализации  и независимы, если t ¹ s. Тогда его можно представить как последовательность {,t = ..., -1, 0, 1, ...} независимых, одинаково распределенных случайных величин. В этом случае ковариационная функция определяется из соотношения

.

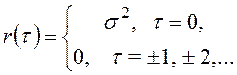Процесс с такой ковариационной функцией называется дискретным "белым шумом". Из (4.7) следует, что его спектральная плотность равна j (w) = s²/(2p), т. е. она постоянна на всех частотах.

"Белый шум" играет важную роль в стохастической теории управления, так как любой случайный процесс можно получить на выходе динамической системы, входной сигнал которой является "белым шумом". Поэтому "белый шум" здесь играет ту же роль, что и прямоугольные импульсы в детерминированных системах.

Формирующие фильтры. Пусть {, k = ... , -1, 0, 1, ...} - дискретный "белый шум". Линейная система (формирующий фильтр), на вход которой подается "белый шум", генерирует широкий класс процессов.

В частности, стохастический процесс

называется скользящим средним, или СС-процессом.

Стохастический процесс , вырабатываемый линейной системой

называется авторегресионным, или АР-процессом.

Стохастический процесс , вырабатываемый системой

называется авторегрессионным процессом со скользящим средним, илиАРСС-процессом.

2. Самостоятельное решение задач

1.  Задача 1. Определите вероятностные характеристики (математическое ожидание, дисперсию и ковариационную функцию) стационарного случайного процесса , сформированного датчиком случайных чисел:

;   ;

,

где:

;  .

Постройте график ковариационной функции этого случайного процесса.

Задача 2. Сформируйте случайный процесс  с помощью формулы (11) с параметрами: ; ; ; ; , используя данные примера 1. Постройте график одной из реализаций случайного процесса . Определите вероятностные характеристики (математическое ожидание, дисперсию и ковариационную функцию) стационарного случайного процесса. Постройте график ковариационной функции этого случайного процесса.

Лабораторная работа № 4.

Тема лабораторной работы. Анализ системы управления с идентификацией параметров ПИ-регулятора.

Цель лабораторной работы. Получение практических навыков идентификации параметров ПИ-регулятора с помощью рекуррентного МНК и анализа качества систем управления.

Задание. Функциональная схема системы управления изображена на рисунке 1. Структурные схемы регулятора и измерительного устройства приведены на рисунках 2 и 3.

Рис. 1. Функциональная схема системы управления

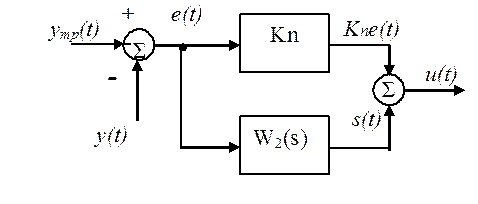
Рис. 2. Структурная схема регулятора

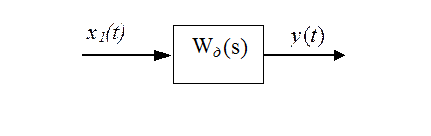
Рис. 3. Структурная схема измерительного устройства

Элементы регулятора и измерительного устройства имеют следующие передаточные функции:

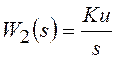;        ;        .                                          (1)

Процессы, происходящие в объекте управления, в пространстве состояний описывают следующими дифференциальными уравнениями с нулевыми начальными условиями:

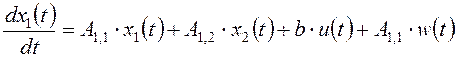;                                (2)