Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 42

При вычислении j(w) по формуле (2.27) значение k определяют, исходя из каких-либо дополнительных соображений. На комплексной плоскости (рис. 2.4) частотная передаточная функция  определяет вектор ОС, длина (модуль) которого равна А(w), а аргумент (угол, образованный этим вектором с действительной положительной полуосью) - j (w). Кривую, которую описывает конец этого вектора при изменении частоты от нуля до бесконечности (иногда от -¥ до ¥ ), называют амплитудно-фазовой частотной характеристикой (АФЧХ).

Частотную передаточную функцию будем называть также амплитудно-фазовой частотной функцией. Ее действительную часть U(w) = Re W(jw) и мнимую часть V(w) = Im W(jw) будем называть соответственно вещественной и мнимой частотными функциями. График вещественной частотной функции (зависимость R(w)) называют вещественной частотной характеристикой, а график A(w)- амплитудной частотной характеристикой.

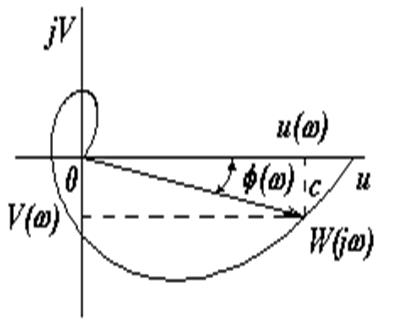
Рис. 2.4.

Аргумент j(w) = arg W(jw) называют фазовой частотной функцией, ее график - фазовой частотной характеристикой.

Кроме перечисленных частотных характеристик, используют еще логарифмические частотные характеристики (ЛЧХ), логарифмические амплитудные частотные характеристики (ЛАЧХ) и логарифмические фазовые частотные характеристики (ЛФЧХ). Назовем функцию

L(w) = 20 lg A(w) = 20 lg ½ W(jw) ½

логарифмической амплитудной частотной функцией. График зависимости логарифмической амплитудной частотной функции L(w) от логарифма частоты (lgw) называют логарифмической амплитудной частотной характеристикой (ЛАЧХ).При построении ЛАЧХ на оси абсцисс откладывают частоту в логарифмическом масштабе на отметке, соответствующей значению lgw, и пишут само значение w, а не значение lgw, а по оси ординат пишут L(w). Логарифмической фазовой частотной характеристикой (ЛФЧХ) называют график зависимости фазовой частотной функции j(w) от логарифма частоты lgw. При его построении по оси абсцисс, как и при построении ЛАЧХ, на отметке, соответствующей значению lgw, пишут значение w.

Единицей измерения L(w) является дицибел, а единицей измерения логарифма частоты в ЛЧХ - декада. Декадой называют интервал, на котором частота изменяется в 10 раз. При изменении частоты в 10 раз говорят, что она изменилась на одну декаду.

Ось ординат при построении ЛЧХ проводят через произвольную точку, а не через точку w = 0. Частоте w = 0 соответствует бесконечно удаленная точка: lgw® -¥ при w® 0.

Таким образом, при гармоническом воздействии в устойчивых системах после окончания переходного процесса выходная величина также изменяется по гармоническому закону, но с другими амплитудой и фазой. При этом отношение амплитуд выходной и входной величин равно модулю, а сдвиг фазы - аргументу частотной передаточной функции. И, следовательно, амплитудная частотная характеристика показывает изменение отношения амплитуд, а фазовая частотная характеристика - сдвиг фазы выходной величины относительно входной, в зависимости от частотного входного гармонического воздействия.

Из приведенной физической интерпретации частотных характеристик ясно, как строить их экспериментальным путем. Для экспериментального построения частотных характеристик имеется специальная аппаратура, в состав которой входят генератор гармонических колебаний с регулируемой частотой и устройства для измерения амплитуды и фазы колебаний.

Разнообразные элементы САУ, имеющие различную конструкцию и функциональное назначение, описываются одинаковыми дифференциальными уравнениями и, следовательно, имеют одинаковые передаточные функции. Коэффициенты, входящие в выражения для передаточных функций, непосредственно связаны с конструктивными параметрами элементов систем регулирования.