Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 70

min E{I} =

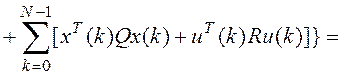
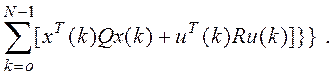
Если минимум функции I существует, то для него справедливо равенство

Таким образом, операция поиска минимума и вычисления математического ожидания коммутативны. Отсюда можно сделать вывод, что стохастические регуляторы должны описываться уравнениями того же типа, что и детерминированные. Следовательно, управление определяется соотношением

Устремив N к бесконечности, получим установившееся решение

Данное выражение описывает стационарный регулятор состояния, принцип действия которого можно пояснить, исходя из следующих соображений. Согласно уравнению (7.21), сигнал управления u(k) должен уменьшать величину x(k+1). Однако как состояние x(k+1), так и управление u(k) зависят только от текущих значений x(k) иv(k) и не зависят от x(k-1),x(k-2), ..., а также от v(k-1), v(k-2), ... . Кроме того, случайное возмущениеv(k) не коррелировано с v(k-1), v(k-2), ... .

Поэтому, при больших значениях N в закон управления должны входить только текущие величины, т. е. u(k) = f(x(k)), и уравнение (7.29) отвечает этому условию. При сравнительно малых значениях N в законе управления необходимо учитывать также случайное начальное состояние x(0) и помеху v(k).

Следовательно, в этом случае необходимо пользоваться нестационарным уравнением оптимального регулятора (7.28). Поскольку оптимизация по отношению к детерминированному начальному состоянию приводит к аналогичному по форме соотношению, оказывается, что уравнение (7.28) описывает регулятор, обеспечивающий оптимальное управление как при детерминированных, так и при случайных помехах (при условии, что в соответствующих критериях качества используются одни и те же весовые матрицы).

Получим теперь выражение для ковариационной матрицы x(k+1) вектора состояния замкнутого контура управления в установившемся режиме. Объединяя соотношения (7.21) и (7.28), запишем уравнение замкнутого контура:

Согласно определению

Это уравнение при k ®¥ дает искомую ковариационную матрицу

Значение критерия качества, которое достигается при включении в контур управления оптимального регулятора состояния, можно определить следующим способом:

E{I_N-1,_N} = E{x^T(N-1)× P_N-1,N×x(N-1)+ v^T×(N-1)×F^T×Q×F×v(N-1)},

E{I_N-1} = E{x^T(N-1)×P_N-1×x(N-1)+ v^T×(N-1)×F^T×Q×F×v(N-1)}

или для N – 2

E{I_N-2} = E{x^T(N-2)×P_N-2×x(N-2) + v^T×(N -2)×F^T×Q×F×v(N-2)} +

+ v^T×(N-1)×F^T×Q×F×v( N-1)}.

Проделаем аналогичным образом все N шагов, учитывая, что v(k) - стационарный случайный процесс:

Обозначим установившееся значение P_o = и возьмем в качестве начального состоянияx(0) случайное возмущение F×v(k). В результате преобразований получим окончательное выражение в виде

7.4. Оптимальные регуляторы с оценкой состояния в случае "белого шума"

В разделе 7.3 предполагалось, что вектор состояния x(k) поддается точному измерению. Однако на практике это далеко не всегда осуществимо, и, как правило, переменные состояния приходится восстанавливать по измеримым координатам системы. Далее будет рассматриваться объект

у которого вектор измерений выхода определяется уравнением

или эквивалентным ему y(k+1)=C×x(k+1)+n(k+1). Считается, что погрешности измерения выходных координат представляют собой векторный "белый шум" со статистиками