Задание.
В динамической системе (например, в социологической системе) в дискретные
моменты времени ![]() в результате действия
контролируемого фактора (входного воздействия)
в результате действия
контролируемого фактора (входного воздействия) ![]() и
возмущающего воздействия
и
возмущающего воздействия ![]() формируются текущие
значения выходной переменной
формируются текущие
значения выходной переменной ![]() анализируемого
процесса. Процессы, происходящие в этой системе, не известны. Функциональная
схема системы сбора информации о текущих значениях входных и выходных
переменных анализируемого процесса изображена на рисунке 1.
анализируемого
процесса. Процессы, происходящие в этой системе, не известны. Функциональная
схема системы сбора информации о текущих значениях входных и выходных
переменных анализируемого процесса изображена на рисунке 1.

Рис. 1. Функциональная схема системы сбора информации о процессе
Выходные переменные измерительных устройств ![]() и
и ![]() связаны
с выходной
связаны
с выходной ![]() и входной
и входной ![]() переменными
анализируемого процесса уравнениями:
переменными
анализируемого процесса уравнениями:
![]() ;
; ![]() ;
; ![]() ;
(1)
;
(1)
![]() ,
(2)
,
(2)
где:
![]() ,
, ![]() -
погрешности измерений, которые не превышают известные пределы допустимых погрешностей
измерений
-
погрешности измерений, которые не превышают известные пределы допустимых погрешностей
измерений ![]() и
и ![]() соответственно;
соответственно;
![]() - шаг квантования времени
- шаг квантования времени ![]() .
.
В системе принятия решений для прогноза значений
выходной переменной ![]() на один шаг используют модель
процесса типа «авторегрессия скользящего среднего» (АРСС):
на один шаг используют модель
процесса типа «авторегрессия скользящего среднего» (АРСС):
![]() ,
(3)
,
(3)
где:
![]() - неизвестный параметр модели процесса;
- неизвестный параметр модели процесса; ![]() - погрешность математической модели анализируемого
процесса.
- погрешность математической модели анализируемого
процесса.
Требуется с помощью
рекуррентного метода наименьших квадратов (РМНК) определить оценки ![]() и
и ![]() возмущающего
воздействия
возмущающего
воздействия ![]() и параметра
и параметра ![]() модели
процесса (1)-(3). Методом имитационного моделирования выполнить анализ
эффективности этого алгоритма идентификации.
модели
процесса (1)-(3). Методом имитационного моделирования выполнить анализ
эффективности этого алгоритма идентификации.
При выполнении лабораторной работы необходимо:
1). Выполнить имитационное моделирование процедуры
сбора информации об изменении контролируемого входного воздействия ![]() и выходной переменной
и выходной переменной ![]() . Для этого необходимо с шагом квантования
времени
. Для этого необходимо с шагом квантования
времени ![]() с. сформировать массивы значений этих
переменных по уравнению (3) с использованием формул:
с. сформировать массивы значений этих
переменных по уравнению (3) с использованием формул:
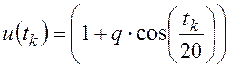 ;
(5)
;
(5)
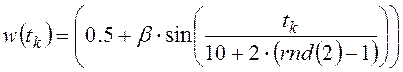 ;
(6)
;
(6)
![]() ;
(7)
;
(7)
![]() .
(8)
.
(8)
При моделировании использовать значения параметров, входящих в уравнения (3), (5)-(8), приведенные в таблице 1.
Таблица 1.
|
№ варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
a |
-0.1 |
-0.2 |
-0.3 |
-0.4 |
-0.5 |
-0.6 |
-0.7 |
-0.8 |
-0.8 |
-0.7 |
-0.1 |
-0.2 |
-0.3 |
-0.4 |
|
b |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.7 |
0.8 |
0.9 |
1.0 |
-1.1 |
-1.2 |
-1.3 |
-1.4 |
|
q |
0.2 |
0.25 |
0.3 |
0.35 |
0.4 |
0.45 |
0.5 |
-0.5 |
-0.4 |
-0.3 |
-0.2 |
0.6 |
0.7 |
0.8 |
|
|
0.7 |
0.65 |
0.6 |
0.55 |
0.5 |
0.45 |
0.4 |
0.35 |
0.3 |
0.25 |
0.2 |
0.15 |
0.1 |
-0.1 |
|
|
0.05 |
0.04 |
0.03 |
0.02 |
0.02 |
0.03 |
0.04 |
0.05 |
0.04 |
0.03 |
0.02 |
0.01 |
0.02 |
0.03 |
|
|
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.04 |
0.03 |
0.02 |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.04 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.