Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 21

4. Передаточные функции и частотные характеристики непрерывных систем управления (СУ).

5. Типовые звенья СУ. Передаточные функции типовых звеньев СУ.

6. Составление передаточной функции СУ по заданному дифференциальному уравнению.

7. Передаточные функции типовых соединений элементов СУ.

8. Функциональные и структурные схемы  СУ. Определение передаточной функции СУ методом преобразования структурных схем.

9. Составление дифференциального уравнения по заданной передаточной функции СУ.

10. Определение частотных характеристик по заданной передаточной функции СУ.

11. Математическая модель непрерывных объектов в пространстве состояний.

12. Математическое описание типовых возмущающих воздействий.

13. Алгоритмы П-, ПИ- и ПИД-регуляторов.

14. Непрерывная модель ПИ-регулятора в пространстве состояний.

15. Непрерывная модель замкнутой системы управления с ПИ-регулятором в пространстве состояний.

16. Общие сведения об устойчивости динамических процессов и систем.

17.  Алгебраический критерий устойчивости непрерывных СУ.

18. Критерий устойчивости Найквиста. Запасы устойчивости по модулю и фазе.

19. Прямые показатели качества управления.

20. Понятие «управляемость системы». Критерий управляемости линейных СУ.

21. Понятие «наблюдаемость системы».  Критерий наблюдаемости линейных СУ.

22. Математическое описание процессов с помощью сплайнов.

23. Функциональная схема цифровой системы управления. Преобразование сигналов в элементах цифровой системы управления.

24. Разностные уравнения модели системы. Разностная модель системы в пространстве состояний.

25. Дискретная передаточная функция. Правила составления дискретной передаточной функции по заданному разностному уравнению.

26. Критерий устойчивости цифровых систем.

27. Идентификация параметров модели системы методом наименьших квадратов.

28. Идентификация параметров модели системы методом максимального правдоподобия. Рекуррентная форма алгоритма метода максимального правдоподобия.

29. Рекуррентный алгоритм оценивания параметров и переменных состояния методом максимального правдоподобия.

30. Модель системы управления с ПИ-регулятором в пространстве состояний.

31. Функционал обобщенной работы в задачах оптимального управления.

32. Настройка параметров ПИ-регулятора рекуррентным методом максимального правдоподобия.

33. Функциональная схема адаптивной системы управления.

ПЕРЕЧЕНЬ ЗАДАЧ

для сдачи экзамена по ТОАУ

1. Составьте передаточную функцию САУ, которая имеет математическую модель

.

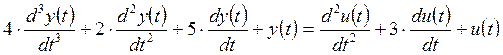2. Составьте передаточную функцию САУ, которая имеет математическую модель

.

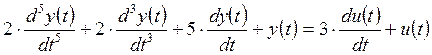3. Составьте передаточную функцию САУ, которая имеет математическую модель

.

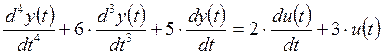4. САУ имеет математическую модель

.

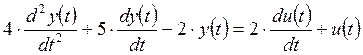Выполните анализ устойчивости САУ.

5. САУ имеет математическую модель

.

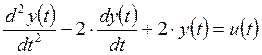Выполните анализ устойчивости САУ.

6. САУ имеет математическую модель

.

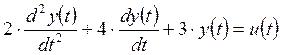Выполните анализ устойчивости САУ.

7. САУ имеет математическую модель

.

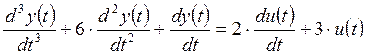Выполните анализ устойчивости САУ.

8. САУ имеет математическую модель

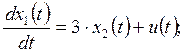
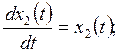
Выполните анализ управляемости САУ.

9. САУ имеет математическую модель

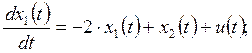
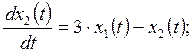
Выполните анализ управляемости САУ.

10. САУ имеет математическую модель

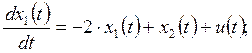
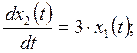
Выполните анализ управляемости САУ.

11. САУ имеет математическую модель

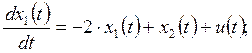
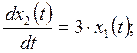
Выполните анализ наблюдаемости САУ.

12. САУ имеет математическую модель

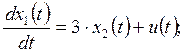
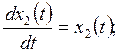
Выполните анализ наблюдаемости САУ.

13. САУ имеет математическую модель

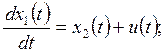
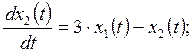
Выполните анализ наблюдаемости САУ.

14. Изобразите структурную схему и определите передаточную функцию системы, образованную 4 звеньями. Входной сигнал  поступает на вход звена №1 с передаточной функцией .  Звенья №2 и №3, которые имеют передаточные функции  и , соединены параллельно. Входы звеньев №2 и №3 соединены с выходом звена №1, а выходы звеньев №2 и №3 соединены с входом звена №4. Звено №4 имеет передаточную функцию .  Выходной сигнал звена №4 является выходным сигналом системы .