Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 62

Выше говорилось, что входное воздействие не может влиять на неуправляемую часть системы. Покажем, что введение обратной связи также не позволяет устранить эту трудность.

Рассмотрим структурную схему системы с обратной связью (рис. 5.13), состоящую из управляемой S₁ и неуправляемой S₂ частей.

Уравнения системы в разомкнутом состоянии

Учитывая, что e=g - y, уравнения системы в замкнутом состоянии

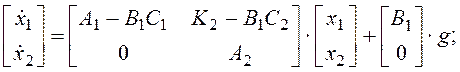
y = [C₁C₂]×[x₁x₂]^T.

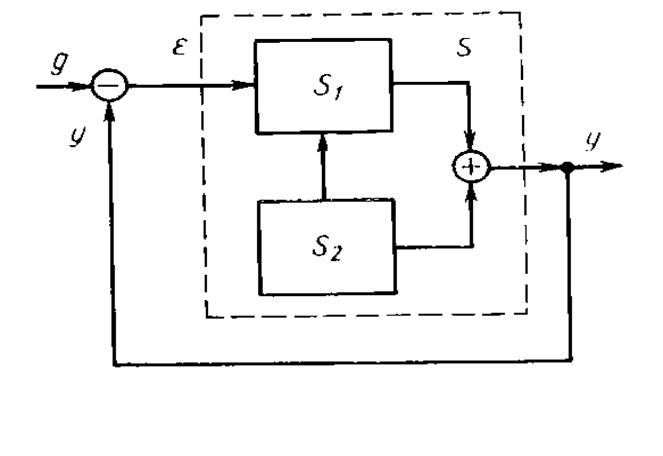
Рис. 5.13.

При этом ее характеристическое уравнение

det [s×I - A₁+ B₁×C₁]× det [s×I - A₂] = 0.

Корни последнего уравнения состоят из корней управляемой части замкнутой системы (первый множитель) и неуправляемой части разомкнутой системы (второй множитель).

Таким образом, введение обратной связи не повлияло на динамику неуправляемой части. К аналогичному выводу можно прийти и по отношению к ненаблюдаемой части.

5.5. Примеры и задачи

Пример. 5.1. Рассмотрим систему S, образованную подсистемами S_a и S_b. Пусть подсистемы имеют следующее математическое описание:

y_1a = x_1a;

y_2a = x_1a;

y₁ = x_1b.

Тогда уравнения системы S  в пространстве состояний имеют вид

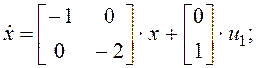
y₁ = [0  1]×x,

из которых видно, что система S неуправляемая и ненаблюдаемая.

Глава 6. АНАЛИЗ УСТОЙЧИВОСТИ САУ

6.1. Основные понятия термина "устойчивость"

Одной из основных задач теории автоматического управления является изучение динамических процессов, происходящих в системах управления. САУ всегда подвергается действию внешних возмущающих сил, которые могут вывести систему из состояния равновесия. Устойчивость САУ является одним из основных условий ее работоспособности и включает требование затухания во времени переходных процессов. Система с расходящимся процессом будет неработоспособной.

В простейшем случае понятие "устойчивость" системы связано со способностью ее возвращаться (с определенной точностью) в состояние равновесия после исчезновения внешних сил, которые вывели систему из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, либо совершает вокруг него недопустимо большие колебания.

Наглядно устойчивость равновесия представлена на рисунке 3.1, где изображен шар, расположенный в некотором углублении (рис. 3.1, а), на некоторой выпуклой поверхности (рис. 3.1, б), на плоскости (рис. 3.1, в).

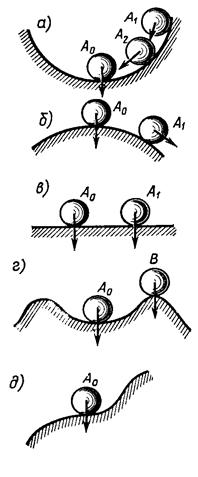
Рис. 3.1.

Положение равновесия шара характеризуется точкой A₀. В случае, изображенном на рисунке 3.1, а, при всяком отклонении шара от положения равновесия, например, в точку A₁, он будет стремиться возвратиться к положению равновесия - в точку A₀ (при отсутствии сил трения) или к некоторой конечной области, окружающей положение равновесия, например в точку A₂ (при наличии сил трения). Такое положение равновесия устойчиво. Случай, изображенный на рисунке 3.1, б, соответствует неустойчивому положению равновесия. Рисунок 3.1, в соответствует нейтральному (безразличному) положению равновесия. На рисунке 3.1, г сотояниеравновесия устойчиво лишь до тех пор, пока отклонение не вышло за некоторую границу, определенную, например, точкой B.

Поэтому в общем случае, рассматривая нелинейные системы, вводят термины "устойчивость в малом", "устойчивость в большом" и " устойчивость в целом".

Система"устойчива в малом", если констатируют лишь факт наличия области устойчивости, но не определяют каким-либо образом ее границы (рис 3.1, г). Систему называют "устойчивой в большом", когда определены границы области устойчивости, т. е. определены границы области начальных отклонений, при которых система возвращается в исходное состояние, и выяснено, что реальные начальные отклонения принадлежат этой области. В том случае, когда система возвращается в исходное состояние при любых начальных отклонениях, систему называют "устойчивой в целом" (рис 3.1, а). "Устойчивость в целом" для определенного класса нелинейностей называют "абсолютной устойчивостью". Очевидно, что система, "устойчивая в целом", будет "устойчива в большом" и " устойчива в малом"; система, "устойчивая в большом", будет "устойчива в малом".