Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 40

где y₀(t) - заданный закон изменения управляемой переменной.

Уравнение (2.11) называют дифференциальным уравнением САУ в отклонениях.

Система линейных дифференциальных уравнений в отклонениях, составленных для  каждой управляемой переменной, совместно с уравнениями, описывающими изменение во времени внешних возмущающих воздействий, дает полное математическое описание САУ. Однако, как уже указывалось, при решении некоторых задач анализа и синтеза САУ удобнее пользоваться другими формами записи математической модели этой же САУ. В частности, при анализе управляемости, наблюдаемости, качества управления и в других задачах применяют математическую модель САУ в пространстве состояний.

2.6. Математическая модель САУ в пространстве состояний

Метод переменных состояния основан на понятии состояние системы. Состояние динамической системы описывают совокупностью физических переменных x₁(t),...,x_n(t), связанных с ее выходными сигналами известными функциональными зависимостями и характеризующих поведение системы в будущем при условии, что известны входные сигналы и состояние системы в исходный момент времени. Переменные состояния x₁(t),...,x_n(t) выбирают таким образом, чтобы можно было математическую модель САУ представить в виде системы дифференциальных уравнений первого порядка с известными значениями x₁(t_o), x₂(t_o),...,x_n(t_o) этих переменных в начальный момент времени t_o (начальными значениями). Тогда интегрированием этой системы (при заданных управляющем u(t) и внешнем w(t) воздействиях) можно определить будущие значения переменных состояния x₁(t),...,x_n(t) и выходной (управляемой) переменной y(t) в произвольный момент времени t.

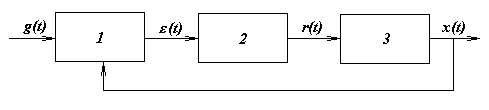
Рис. 2.3.

Поясним понятие переменных состояния на примере САУ, состоящей (рис. 2.3) из задатчика 1, объекта управления 3, измерительного устройства (ИУ) и П-регулятора 2.

Пусть ОУ имеет математическую модель

а выходной сигнал ИУ z(t) связан с управляемой переменной y(t) уравнением

Математическую модель П-регулятора описывают уравнением

Введем новые переменные

В новых переменных математическую модель (2.12) - (2.14) можно преобразовать в следующую эквивалентную систему уравнений, включающую дифференциальные уравнения первого порядка

и алгебраическое уравнение (уравнение наблюдения)

где

Переменные x₁(t) и x₂(t) называют переменными состояния объекта, а уравнения (2.16) - (2.17) - математической моделью САУ в пространстве состояний.

Уравнения (2.16), (2.17) можно записать в компактной матричной форме

; ; ; ; .

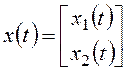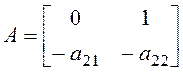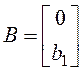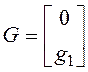Линейную модель САУ (2.11) также можно описать в пространстве состояний матричными уравнениями

если в матрицу-столбец x(t) включить n переменных состояния x_j(t),.(j=1,2,...,n). В этом случае A - квадратная [n´n] матрица, B и G - матрицы-столбцы, u(t), f(t) и z(t) - скалярные переменные, C - матрица-строка.

В общем случае линейную САУ с несколькими управляющими воздействиями и несколькими возмущающими воздействиями также можно описать в пространстве состояний матричными уравнениями (2.18). Но в этом случае A - квадратная [n´n] матрица, B, C и G - прямоугольные матрицы, u(t), f(t) и z(t) - матрицы-столбцы. При этом матрицы A, B, C и G могут быть известными матричными функциями времени.

Матрицу-столбец x(t), содержащую все переменные состояния x_j(t) (j=1,2,...,n), называют вектором состояния САУ.

Решение матричного дифференциального уравнения (2.18) можно получить на ЭВМ с помощью стандартных программ, входящих в их математическое обеспечение.