Другие предметы \ Теоретические основы автоматизированного управления

Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 69

P(tj) = S

(7.13)

Таким образом, решение матричного уравнения Риккати можно проводить в обратном направлении, от tj к to, построив матрицу

K(t) = -R-1 (t) BT (t) P (t)

(7.14)

и получив затем управление по замкнутому контуру из

u (t) = + K (t) x (t)

(7.15)

Важно отметить, что все составляющие вектора состояния должны быть достижимыми.

Вычисляя вторую вариацию, получим

(7.16)

Таким образом, для доказательства достаточного условия минимума необходимо, чтобы матрицыQ, R и S были, по крайней мере, положительно полуопределенными. Кроме того, из (7.7) следует, что матрица Rдолжна иметь обратную матрицу. Таким образом, достаточно, чтобы матрица R была положительно определенной, а матрицы Qи S - по крайней мере, положительно полуопределенными.

В ряде случаев может оказаться, что некоторые элементы матрицы Sдостаточно велики, что приводит к затруднению вычислений. В таких случаях возможно и, по-видимому, желательно получить “инверсное” дифференциальное уравнение Риккати. Положим

P (t)×P-1 (t) = I

(7.17)

и после дифференцирования получим

(7.18)

т. е. получим “инверсное” уравнение Риккати

                            

(7.19)

с граничным условием

P-1 (tj) = S-1.

(7.20)

Таким образом, например, можно решить уравнение Риккати так, чтобыS-1была нулевой матрицей, для чего необходимо, чтобы каждая компонента вектора состояния достигла начала в момент достижения границы. “Усиление”K(t) или хотя бы некоторые его компоненты в этом случае в момент достижения границы становятся бесконечными.

Можно записать нелинейное матричное управление Риккати размерности n ´ n при граничном условии как 2´ n-мерное векторное линейное дифференциальное уравнение с двухточечными граничными условиями.

7.3. Оптимальные дискретные регуляторы состояния в случае "белого шума"

Рассмотрим дискретную модель объекта

x (k + 1) = Ax (k) + Bu (k) + Fv (k).

(7.21)

Предполагается, что помеха v(k) распределена по нормальному закону с математическим ожиданием

E {v (k)} = 0

(7.22)

и ковариационной матрицей

cov [v (k), t = i - j] = E {v (i)× vT (j)} = Vdij,

(7.23)

где dij - функция Кронекера, причем

dij =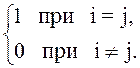

Кроме того, будем полагать, что сигнал помехиv(k) не зависит от вектора состояния x(k), а начальное состояние х(0) также случайно и распределено по нормальному закону со статистиками

E {x (0)} = 0;

cov [x (0)] = E {x (0) xT (0)} = X0.

(7.24)

Матрицы ковариаций V и Xo положительно полуопределены. Нашей целью является построение регулятора, вырабатывающего последовательность входных сигналовu(k), формируемых на основе векторов состояния x(k), все координаты которых доступны непосредственному измерению. Эта последовательность сигналов, обращая в минимум квадратичный критерий качества

E{I} = E

(7.25)

должна обеспечивать достижение конечного состояния x(N) »0.

Предполагается, что в выражении (7.25)Qявляется симметрической положительно-полуопределенной матрицей, а R - симметрической положительно-определенной. Поскольку и переменные состояния, и входные сигналы в модели (7.1) случайны, значение критерия качества I также представляет собой случайную величину. Ввиду этого минимизации подвергается не сама функция I, а ее математическое ожидание (7.25).

Сначала получим закон управления, в котором не участвуют выходная переменная y(k). Случай, когда переменные состояния не поддаются измерению и для управления используются измеримые, но содержащие случайные погрешности значения выходной переменной, будет рассмотрен в разделе 7.4. Первые публикации, посвященных исследованию стохастических регуляторов состояния, относятся к 1961 г.

Для получения оптимальной последовательности входных сигналов u(k) воспользуемся принципом максимума Понтрягина, изложенным в разделе 7.2:

Скачать файл