Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 67

Для того чтобы в системе отсутствовали расходящиеся колебательные процессы, необходимо, чтобы были положительны главные определители матрицы Гурвица (или должны выполняться условия критерия Рауса). Однако применение данных критериев к системам порядка выше второго вызывает необходимость в применении ЭВМ, поскольку для его проверки необходимо вычислять определители матрицы Гурвица высокого порядка. Поэтому эти критерии не имеют существенных преимуществ перед рассмотренным ранее методом анализа устойчивости по корням характеристического уравнения.

6.6. Примеры и упражнения

Пример 6.1. Передаточная функция дискретной системы второго порядка имеет знаменатель

A(z) = z² + a₁z + a₂.

После подстановки 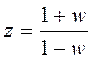 имеем

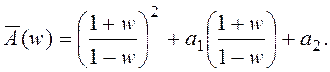
Полученное выражение запишем в виде

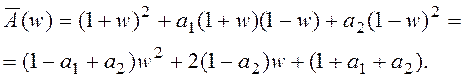
Если для системы второго порядка выполняются  условия

A(- 1) = 1 - a₁ + a₂ >0;

 A(1) = 1+ a₁ + a₂>0;

  a₂<1,

то все коэффициенты  строго положительны.

Глава 7. ОПТИМАЛЬНОЕ  УПРАВЛЕНИЕ  СИСТЕМАМИ

7.1. Задачи оптимального управления

В конце 50-х г. Р. Беллман и Л.С. Понтрягин показали, что многие задачи проектирования могут быть сформулированы как задачи оптимизации. Для нелинейных систем это привело к неклассическому вариационному исчислению. Беллманом было найдено точное решение для линейных систем с квадратичными функциями потерь. В своей знаменитой работе Р. Калман доказал, что линейная квадратичная задача сводится к решению дифференциального уравнения Риккати. Он также показал, что классическая задача фильтрации Н. Винера может быть переформулирована в рамках теории пространства состояний. Это позволило добиться "решения" с помощью рекурсивных уравнений, очень удобных для решения на ЭВМ.

В частности, задача может заключаться в максимизации дальности полета ракеты, максимизации доходов какого-либо предприятия, минимизации ошибки оценивания координат объекта, минимизации энергии или затрат, требуемых для достижения некоторого заданного конечного состояния. Можно указать множество аналогичных задач. Исследование управления, с помощью которого может быть достигнута заданная цель при условии минимизации (или максимизации) определенного критерия качества системы, составляет фундаментальную задачу теории оптимизации.

Эта задача может быть разделена на четыре взаимосвязанные части:

1. Определение цели.

2. Определение положения системы относительно цели.

3. Определение внешних факторов, оказывающих влияние на прошлое, настоящее и будущее системы.

4. Выбор наилучшей тактики поведения, исходя из определения цели (1), знания текущего состояния (2) и внешних факторов (3).

Для решения задачи оптимизации в первую очередь необходимо определить целевую или стоимостную функцию оптимизируемого процесса. При этом требуется дать соответствующую формулировку задачи в физической форме и осуществить перевод этого физического описания на язык математики. Для осуществления эффективного управления процессом необходимо знать его текущее состояние. Будем называть это задачей оценки состояния. Кроме того, необходимо охарактеризовать процесс с помощью адекватной модели, зависящей от различных внешних факторов. Будем называть это идентификацией системы. При условии знания функции стоимости, состояния и параметров системы можно затем определить наилучшее управление, минимизирующее (или максимизирующее) функцию стоимости. Таким образом, можно сформулировать пять взаимосвязанных задач, решение которых даст возможность построить наилучшую, или оптимальную, систему.

1. Задача управления. Рассматривается система с заданной связью между входным управляющим воздействием и состояниями системы. Требуется найти управление, меняющее состояние x(t) так, чтобы была достигнута некоторая заданная цель. Это может быть задача с замкнутым или разомкнутым контуром в зависимости от того, является ли управление функцией состояния системы.