Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 48

2. Выбор структуры системы управления. Описав математическую модель объекта управления и задав соответствующий набор управляемых переменных, проектировщик должен определить тип системы управления. Существуют, в частности, следующие типы систем управления:

- с одним входом и одним выходом;

- с перекрестными связями;

- со многими входами и многими выходами.

3. Разработка алгоритмов для управления в прямой цепи и цепях обратных связей (синтез и настройка). Завершающим этапом проектирования является синтез алгоритмов управления в цепях прямой и обратных связей, а также их настройка (или подстройка) с учетом конкретных условий функционирования системы. Настройку можно выполнять различными способами:

- проводя подстройку параметров вручную, руководствуясь несложными правилами;

- с помощью автоматизированного расчета на ЭВМ;

- используя адаптивные алгоритмы управления.

Как правило, применяя различные методы синтеза, можно получить несколько алгоритмов управления, отличающихся по своим характеристикам. Среди них необходимо выбрать наилучший, исходя из совокупности различных показателей.

4. Фильтрация шумов. Высокочастотные шумы, вносящие помехи в измерения управляемых переменных, но сами недоступные измерению, должны подавляться с помощью аналоговых и цифровых фильтров.

5. Корректирующие алгоритмы в прямых цепях и цепях обратных связей исполнительных устройств. В цепях прямых и обратных связей исполнительных устройств в зависимости от их конструкции могут применяться различные алгоритмы коррекции. При разработке алгоритмов управления объектом следует учитывать динамические свойства корректирующих алгоритмов.

Работоспособность всех алгоритмов управления и фильтрации должна анализироваться с учетом эффектов квантования по уровню. На рисунке 3.4 представлена общая схема процесса проектирования цифровых систем управления. Если для параметрической оптимизации простых алгоритмов управления применяются несложные процедуры подстройки параметров, то можно ограничиться простейшими моделями объектов. При проведении однократного расчета алгоритмов на ЭВМ необходимы точные модели объектов управления и сигналов, для формирования которых наиболее целесообразно использовать методы идентификации и оценивания параметров. Если же процесс получения информации и расчета алгоритма управления носит непрерывный характер и может протекать в реальном времени, возможно построение адаптивной системы управления.

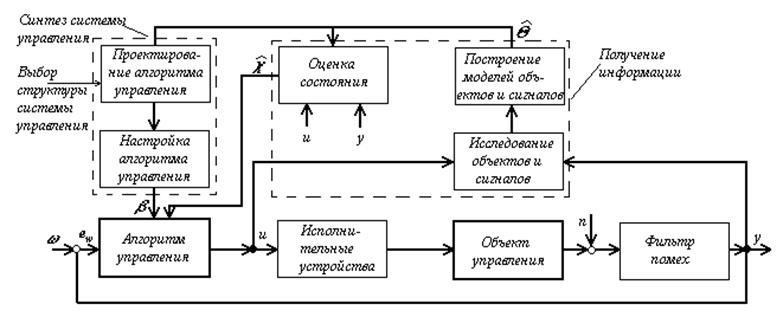
Рис. 3.4.

3.2. Дискретные по времени функциии разностные уравнения

Дискретность (и, следовательно, разрывность) сигналов обусловлена их квантованием по уровню и (или) по времени. В противоположность непрерывным сигналам, которые описываются непрерывными функциями времени, дискретные сигналы могут принимать лишь дискретные значения в дискретные моменты времени. В дальнейшем будут рассматриваться сигналы, дискретные только во временной области. Они представляют собой последовательности импульсов, появляющихся в определенные моменты времени. Обычно дискретный сигнал получается в результате периодического прерывания непрерывного сигнала с постоянным тактом.

Существуют разные способы модуляции отдельных импульсов, входящих в последовательность. Они отличаются допустимыми значениями амплитуд, шириной импульсов и модулирующей частотой. В цифровых системах управления обычно применяется лишь амплитудная модуляция импульсов, причем в основном тот ее вариант, при котором высота импульса пропорциональна текущему значению непрерывного сигнала, ширина постоянна, а интервалы между импульсами одинаковы и равны такту квантования (рис. 3.5). Поскольку к дискретным сигналам этого типа применима теорема суперпозиции, они описываются линейными соотношениями, аналогичными по форме уравнениям линейных динамических систем. Рисунок 3.5 иллюстрирует принцип получения последовательности импульсов, основанный на пропускании непрерывного сигнала x(t) через ключ, который периодически, с тактом квантования T₀, замыкается на время h. Если длительность импульса h существенно меньше такта квантования T₀, а за ключом стоит линейное звено с постоянной времени T_i  h, то последовательность импульсов x_p(t) можно приближенно рассматривать как дискретный сигнал x_T(kT₀), показанный на рисунке 3.6. В этом случае ключ действует как идеальный квантователь, и величины x_T(kT₀)равны мгновенным значениям амплитуд.