7. Моделированием на ЭВМ построить графики переходных
процессов для переменных состояния ![]() и
и ![]() объекта управления (
объекта управления (![]() =0, 1, …, N). При
моделировании считать, что требуемый закон изменения управляемой переменной задан
формулой:
=0, 1, …, N). При
моделировании считать, что требуемый закон изменения управляемой переменной задан
формулой:
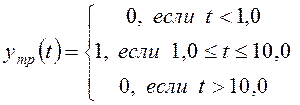 . (4)
. (4)
8. Составить отчет.
Методические указания к выполнению задания
Система управления имеет следующую модель:
![]() ;
; ![]() . (a)
. (a)
![]() . (b)
. (b)
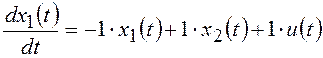 ;
(c)
;
(c)
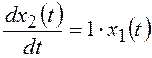 .
(d)
.
(d)
1. Из уравнений (с) и (d) видно, что объект управления
имеет 2 переменные состояния: ![]() и
и ![]() .
.
Из структурной схемы измерительного устройства (рис. 3) следует, что выходной сигнал измерительного устройства связан с переменными состояния объекта управления уравнением наблюдения:
![]() .
.
Поэтому система, образованная объектом управления и измерительным устройством, имеет следующую модель в пространстве состояний:
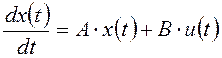 ;
(I)
;
(I)
![]() ,
(II)
,
(II)
где: 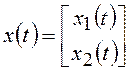 ;
; 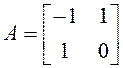 ;
; 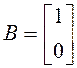 ;
; ![]() .
.
2. Выполним преобразование Лапласа правой и левой частей уравнения (1):
![]() .
(1a)
.
(1a)
Из определения понятия "передаточная функция звена" и уравнения (1a) определим передаточную функцию регулятора:
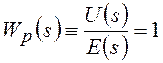 .
.
3. Выполним преобразование Лапласа правой и левой частей уравнения (2):
![]() .
(2a)
.
(2a)
Из определения понятия "передаточная функция звена" и уравнения (1a) определим передаточную функцию измерительного устройства:
 .
.
4. Для составления передаточной функции объекта
управления из уравнений (с) и (d) исключим переменную ![]() :
:
![]() .
.
Или:
![]() .
.
Поэтому передаточная функция объекта управления определяется так:
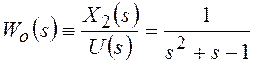 .
.
5. Из схемы системы управления (рис. 1) видно, что передаточная функция прямой цепи
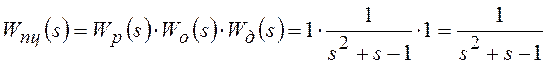 .
.
Передаточная
функция разомкнутой цепи ![]() , поэтому передаточная
функция системы управления (с отрицательной обратной связью)
, поэтому передаточная
функция системы управления (с отрицательной обратной связью)
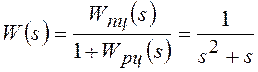 .
.
6. Составим дискретную модель системы управления
методом Эйлера. Для этого выполним квантование времени с постоянным шагом ![]() по формуле:
по формуле:
![]() ;
; ![]() .
.
В дискретный момент времени ![]() заменим
производные по времени приближенными выражениями:
заменим
производные по времени приближенными выражениями:
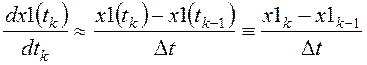 ;
;
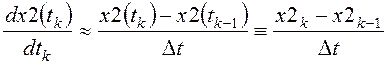 .
.
В правых частях дифференциальных уравнений в
дискретный момент времени ![]() будем использовать
приближенные значения переменных:
будем использовать
приближенные значения переменных:
![]() ;
; ![]() ;
; ![]() .
.
В результате получим следующую систему разностных уравнений:
![]() ;
;
![]() ; (f)
; (f)
![]() ;
;
![]() ; (g)
; (g)
![]() ;
k=1, 2, …, N. (l)
;
k=1, 2, …, N. (l)
7. Для построения графиков переходных процессов необходимо решить на ЭВМ систему уравнений (f), (g), (l), (4) с помощью математического пакета Mathcad.
Построить графики переходных процессов для переменных
состояния объекта управления ![]() и
и ![]() .
.
8. Составить отчет по результатам выполнения задания (пояснения к п.п. 1-7 методических указаний).
Лабораторная работа № 2.
Тема лабораторной работы. Анализ САУ с цифровым регулятором.
Цель лабораторной работы. Получение практических навыков анализа систем управления.
Задание. Функциональная схема системы управления изображена на рисунке 1.
Структурные схемы регулятора и измерительного устройства приведены на рисунках 2 и 3.

Рис. 1. Функциональная схема системы управления
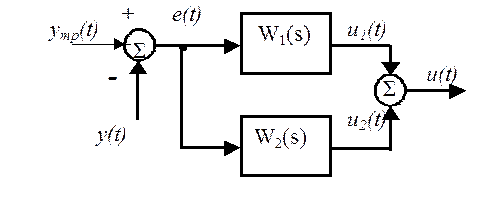
Рис. 2. Структурная схема регулятора
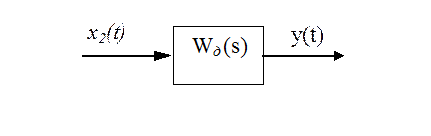
Рис. 3. Структурная схема измерительного устройства
Элементы регулятора и измерительного устройства имеют следующие передаточные функции:
![]() ;
;
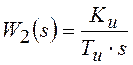 ;
; ![]() .
(1)
.
(1)
Процессы, происходящие в объекте управления, в пространстве состояний описывают следующими дифференциальными уравнениями с нулевыми начальными условиями:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.