Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 73

- рекуррентный метод наименьших квадратов;

- метод фильтрации с минимальной дисперсией;

- метод максимального правдоподобия;

- метод Байеса.

Ниже для построения алгоритма будет использован рекуррентный метод оценивания с минимальной дисперсией. Он наиболее удобен, поскольку не требует никаких предварительных теоретических выкладок и допускает простую и наглядную интерпретацию результатов.

Взвешенное усреднение двух векторных величин.Алгоритм оценивания, известный как фильтр Калмана, формирует взвешенное среднее двух независимых векторных оценок. Предположим, для некоторого m-мерного вектора х найдены две статистически независимыеоценких₁и х₂. Их взвешенным средним назовем величину

где K - это весовая матрица (m´ m), которая выбирается таким образом, чтобы дисперсия оценки  была минимальна. Далее будет рассматриваться динамическая система, для которой в качестве x_iберется ее вектор состояний размерностиm. Вместо x₂ будет использован вектор выходных измеренийy₂ размерности p < m, связанный с x₂ соотношением

С учетом этого уравнение (7.61) принимает вид

Случайный вектор x_i имеет ковариационную матрицу

вектор y₂ - ковариационную матрицу

Воспользовавшись условием статистической независимости x₁ и y₂, введем формулу для ковариационной матрицы оценки  в (7.63):

Найдем теперь такую матрицу К, которая минимизировала бы дисперсии ошибок оценивания (т. е. диагональные элементы матрицыР). Для того чтобы определить ее, не прибегая к дифференцированию, несколько преобразуем уравнение (7.66). Выполним умножение, учитывая, что Q = Q^T, поскольку Q - симметрическая матрица:

В уравнении (7.67) желательно выделить слагаемое, являющееся полным квадратом относительноК. С этой целью введем две новые матрицы R и S, такие, что

Положив в (7.68)

приходим к выражению

Правая часть данного выражения совпадает с разностью (P - Q), полученной из (7.67). Исключение составляет лишь член RR^T, который можно определить, воспользовавшись уравнениями (7.69) и (7.71):

S^TSR^T = S^T CQ; R^T  = (S^TS)^-1 S^TCQ; R = QC^TS (S^TS)^-1;

RR^T = QC^T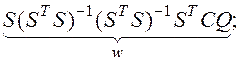

S^TWS = (S^TS) (S^TS)^-1 (S^TS)^-1 (S^TS) = I; SS^TWSS^T = SIS^T = SS^T.

Таким образом,

W = (SS^T)^-1.

Согласно (7.69), отсюда следует

Подставляя (7.71) и (7.72) в уравнение (7.67), получаем окончательно

В уравнении (7.73) только слагаемое (KS – R)× (KS - R)^T зависит от К. Диагональные элементы этой матрицы, равные квадратам соответствующих элементов        (KS- R), всегда больше или равны нулю. Следовательно, диагональные элементы Р достигают минимума при KS - R = 0. Отсюда, используя (7.69) и (7.70), можно записать

Ковариационная матрица оценки с минимальной дисперсией, согласно (7.67), определяется выражением

а сама оценка имеет вид

гдеКнаходится из уравнения (7.74).

Рекуррентный алгоритм оценивания вектора состояния.Применим процедуру определения взвешенного среднего двух векторных величин, описанную в предыдущем разделе, к оцениванию вектора состояния (k+1) марковского процесса (7.59), (7.60). Для этого преобразуем переменные, участвующие в уравнении (7.63):