Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 79

получим ограниченный выход, так как п ограничено, - противоречие.

Самонастраивающийся регулятор (8.12)-(8.13) всегда стабилизирует систему (8.14) в среднеквадратическом смысле. Можно показать, что оценка параметра  также сходится к точному значению. Если последовательность сходится при k®¥, то легко найти ее предел. Нормальное уравнение можно записать в виде

.

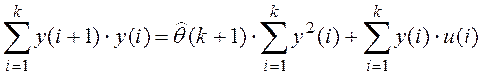Тогда из (8.13) следует, что

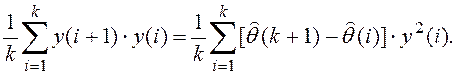
Правая часть этого уравнения стремится к нулю при k®¥, поскольку  сходится, а у(k) ограничено в смысле (8.16). Таким образом, если сходится, то

Итак, самонастраивающийся регулятор стремится свести к нулю автокорреляцию в замкнутой системе, r_y(t), для t =1. Предположив теперь, что регулируемый процесс описывается уравнением (8.8), получим, что (8.16) ограничено и (8.17) имеет место лишь при одном значении , а именно приq =а - с.

Таким образом, регулятор (8.12)—(8.13) для системы (8.8) с функционалом (8.9) самонастраивается. Этот результат остается в силе и при b ¹1. Более того, его можно обобщить на случай процессов п-го порядка вида (8.7). Однако для получения устойчивости и сходимости по управлению необходимо ввести дополнительные ограничения. Более того, в многомерном случае последовательность оценок параметров может и не сходиться.

Общие результаты. Анализ этого простого примера можно обобщить. Некоторые асимптотические свойства самонастраивающихся регуляторов можно сформулировать в виде следующих теорем.

Теорема 8.1. Рассмотрим алгоритм 8.2, и пусть . Предположим, что оценки параметров s_i, i = 0, ..., n_s и r_i = 1, .... n^r сходятся и что замкнутая система эргодическая (по моментам второго порядка). Тогда замкнутая система обладает следующими свойствами:

E{y(k + t)y(k)} = r_y(t) = 0, t = d, ..., d+ n_s,

E{y(k + t)y(k)} = r_yu(t) = 0, t = d, ..., d+ n_r.

Теорема 8.2. Пусть управляемая система описывается уравнением (8.7), где  известно. Предположим, что используется алгоритм 8.2, где n_s ³п - 1 и n_r ³п+d - 1. Если последовательность оценок параметров сходится, то регулятор (8.3) с Т=0 сходится к регулятору, минимизирующему дисперсию ошибки для процесса (8.7).

Из теоремы 8.1 следует, что в стационарных точках алгоритма некоторые значения r_у(t) и r_уи(t) обращаются в нуль. При этом конкретный вид процесса не играет роли. Теорема 8.2 утверждает, что если процесс описывается уравнением (8.7) с известным значением d, то самонастраивающийся регулятор с достаточно большим числом параметров сходится к предельному регулятору, минимизирующему дисперсию ошибки, если он сходится вообще.

Можно проанализировать устойчивость и свойства сходимости самонастраивающихся регуляторов. Можно также показать, что если выражение    

1/С(z) – 1/2

 действительно и строго положительно, то самонастраивающийся регулятор с оценкой параметров по методу наименьших квадратов и с функционалом (8.9) реализует оптимальное управление для процесса (8.7). Если С(z_i) > 0 для z_i, таких что B( z_i) = 0, то алгоритм локально устойчив.

8.6. Другие подходы к адаптивному управлению

Структура самонастраивающегося регулятора, описанного в разделе 8.1, предполагает наличие  самонастраивающегося контура управления. Вместе с тем можно ожидать, что регулятор, показанный на рисунке 8.1, может быть использован для управления процессом с переменными параметрами, т. е. для адаптивного управления. Для этого, однако, необходимо несколько изменить алгоритм так, чтобы блок оценки параметров мог отслеживать изменение параметров процесса. Один из способов решения этой задачи состоит в дисконтировании старых данных. Есть, однако, и другие схемы реализации адаптивного управления, более близкие к идее самонастраивающегося регулирования, в которых параметры регуляторов изменяются в зависимости от изменения состояния процесса и возмущений.