Регулятор, показанный на рисунке 8.1, можно получить, следуя идеям регулирования по эталонной модели, если для оценки параметров использовать коррекцию последней. Такую схему называют неявной схемой адаптивного регулирования по эталонной модели, поскольку здесь параметры регулятора корректируются не непосредственно, а через модель. Явная схема АРЭМ, где осуществляется непосредственная корректировка параметров регулятора, тесно связана с неявными СНР и наоборот.
Стохастическая теория управления. Регуляторы типа СНР и АРЭМ строятся на основе эвристических рассуждений, поэтому хотелось бы попытаться прийти к ним на основе некоторого единого теоретического подхода. Таким подходом является теория нелинейного стохастического управления, в которой сама система и внешние воздействия описываются некоторой стохастической моделью. При этом цель управления состоит в минимизации математического ожидания функции потерь, являющейся скалярной функцией от переменных состояния и управлений.
Задача отыскания управления, минимизирующего математическое ожидание функции потерь, весьма сложна: на самом деле не известны даже условия существования решения этой задачи. Если, однако, предположить, что решение существует, то, воспользовавшись методом динамического программирования, можно вывести некоторое функциональное уравнение для оптимального значения функционала. Это уравнение, называемое уравнением Беллмана, можно решить численно только в самых простых случаях.
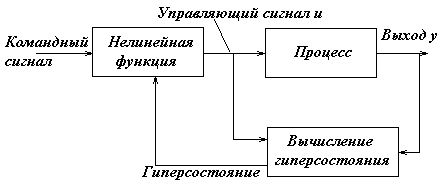
Рис. 8.5.
Структура полученного таким образом оптимального регулятора показана на рисунке 8.5. Регулятор фактически состоит из блока оценки параметров и блока синтеза управления. По данным измерениям блок оценки генерирует функцию распределения условных вероятностей переменных состояния, называемую гиперсостоянием системы. Регулятор тогда представляет собой нелинейную функцию, отображающую гиперсостояние на пространство переменных управления.
Структурная простота решения получается ценой введения гиперсостояния, характеризующегося очень высокой размерностью. Заметим, что СНР (рис. 8.1) можно рассматривать как аппроксимацию регулятора, показанного на рисунке 8.5, в которой гиперсостояние заменяется состоянием процесса и оценками параметров.
Оптимальное управление обладает следующим интересным свойством: оно не только приводит выход к заданной величине, но и при наличии неопределенности в значениях параметров вводит некоторые возмущения, которые улучшают полученные оценки. Таким образом, оно одновременно минимизирует ошибки регулирования и величину необходимых управлений. Такое управление называют дуальным.
Самонастраивающиеся и адаптивные методы еще не вышли из "периода младенчества". До появления микропроцессоров практическая реализация этих алгоритмов стоила бы слишком дорого. Тем не менее, поскольку их применение сулит получение новых типов регуляторов и неординарные возможности для систем управления, представляет определенный интерес попытка наметить возможную сферу их использования.
Автоподстройка. Вручную можно подобрать значения трех-четырех параметров регуляторов, если они не слишком сильно связаны между собой. Однако в более сложных случаях регулятор должен иметь специальный механизм настройки. Как правило, настройка параметров достаточно сложного регулятора включает этапы моделирования или идентификации и проектирования. Эта процедура часто весьма дорога и занимает много времени, поэтому к ней прибегают только в случае настройки особо важных элементов или массового производства.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.