2. По критерию наблюдаемости Калмана определить, наблюдаем ли объект управления.
3. Составить передаточную функцию системы управления и по корням характеристического уравнения выполнить анализ устойчивости:
а) системы управления с П-регулятором;
б) системы управления с ПИ-регулятором.
4. Определить функциональные зависимости управляющего
воздействия ![]() от переменных состояния объекта управления
и
от переменных состояния объекта управления
и ![]() для П-регулятора и ПИ-регулятора.
для П-регулятора и ПИ-регулятора.
5. Составить дискретную модель в пространстве состояний (исключив из уравнений (2), (3) управляющее воздействие):
а) системы управления с П-регулятором;
б) системы управления с ПИ-регулятором.
Шаг
квантования времени принять равным ![]() =0,01 с.
=0,01 с.
6. Моделированием на ЭВМ определить графики переходных
процессов для переменных состояния ![]() и
и ![]() объекта управления с П-регулятором и
ПИ-регулятором (
объекта управления с П-регулятором и
ПИ-регулятором (![]() =0, 1, …, N).
При моделировании считать, что требуемый закон изменения выходного сигнала
измерительного устройства задан формулой:
=0, 1, …, N).
При моделировании считать, что требуемый закон изменения выходного сигнала
измерительного устройства задан формулой:
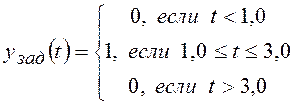 .
(4)
.
(4)
По графикам переходных процессов определить прямые показатели качества регулирования.
7. Составить отчет по лабораторной работе.
Методические указания к выполнению задания
Система управления (рис. 1) имеет следующую модель:
![]() ;
;
![]() ; (a)
; (a)
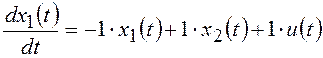 ; (b)
; (b)
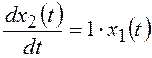 .
(c)
.
(c)
1. Из уравнений (b) и (с) видно,
что объект управления имеет 2 переменные состояния: ![]() и
и ![]() .
.
Из структурной схемы измерительного устройства (рис. 3) следует, что система, образованная объектом управления и измерительным устройством, имеет следующую модель в пространстве состояний:
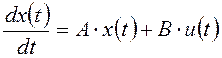 ;
(d)
;
(d)
![]() .
(e)
.
(e)
Составим матрицу управляемости (при n=2):
![]() .
.
Так как
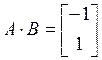 ,
,
то
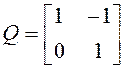 .
.
Ранг матрицы управляемости равен 2, так как эта матрица имеет две строки и два столбца, а ее определитель равен 1.
Таким образом, объект управляем.
2. Составим матрицу наблюдаемости (при n=2):
![]() ,
,
поэтому
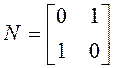 .
.
Ранг матрицы наблюдаемости равен 2, так как эта матрица имеет две строки и два столбца, а ее определитель равен 1.
Таким образом, система "объект – измерительное устройство" наблюдаема.
3. Для составления передаточной функции системы
управления определим передаточную функцию объекта управления. Для этого из
уравнений (b) и (с) исключим переменную ![]() . В
результате получим следующее уравнение:
. В
результате получим следующее уравнение:
![]() .
.
Поэтому передаточная функция объекта управления такова:
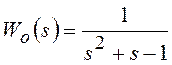 .
.
Из схемы системы управления (рис. 1) видно, что передаточная функция прямой цепи
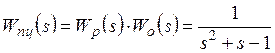 .
.
Передаточная функция разомкнутой цепи
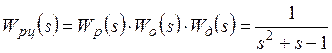 .
.
Передаточная функция системы управления (с отрицательной обратной связью)
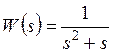 .
.
Составим характеристическое уравнение системы управления:
![]() .
.
Это уравнение имеет действительные корни:
![]() ;
;
![]() .
.
Один корень характеристического уравнения равен нулю, другой – отрицательный. Поэтому по критерию Ляпунова система управления находится на границе устойчивости (в критическом состоянии).
Вывод:Систему управления применять по назначению нельзя.
4. Из рисунка 2 видно, что регулятор имеет следующую модель в пространстве состояний:
![]() .
.
5. Составим дискретную модель системы управления:
![]() ; k=1, 2, …,
N; (f)
; k=1, 2, …,
N; (f)
![]() ;
(g)
;
(g)
![]() .
(l)
.
(l)
6. Решить на ЭВМ систему уравнений (f), (g), (l), (4) с помощью математического пакета Mathcad.
Построить графики переходных процессов для переменных
состояния объекта управления ![]() и
и ![]() . По графикам переходного процесса
определить прямые показатели качества управления (для переменных состояния
. По графикам переходного процесса
определить прямые показатели качества управления (для переменных состояния ![]() и
и ![]() ).
).
Составить отчет по результатам выполнения задания.
1. Дайте определение понятия «передаточная функция системы». Как определить передаточные функции типовых соединений звеньев с известными передаточными функциями?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.