Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 78

Явные алгоритмы.Явные самонастраивающиеся алгоритмы, такие как алгоритм 8.1, сходятся к решению, если оценки параметров сходятся к истинным значениям. Это так, если при оценке параметров используется корректная модель, а входной сигнал имеет достаточно богатый частотный спектр. Кроме того, поскольку при оценивании используется МНК, необходимо, чтобы возмущения были некоррелированы, т. е. чтобы в (8.7) выполнялось условие С = 1. Далее, поскольку управляющий сигнал генерируется звеном обратной связи, для "обогащения" его частотного спектра может потребоваться введение определенных возмущений.

Анализ системы первого порядка. Для иллюстрации принципиальной схемы анализа самонастраивающихся регуляторов начнем с систем первого порядка.

Предположим, что динамика объекта управления и внешние воздействия описываются простой моделью первого порядка:

где и - управляющая переменная, у - выход, a {e(k)} - последовательность независимых нормально распределенных случайных чисел. Предположим, кроме того, что целью управления является минимизация квадратичной функции потерь:

Будем считать, что допустимые управления таковы, что u(k) зависит от всех "прошлых" выходов y(k), y(k - 1), ... . Если параметры модели известны, то оптимальное управление реализуется пропорциональным регулятором

Рассмотрим самонастраивающийся регулятор с настройкой параметра q с помощью МНК по модели:

Среднеквадратическая оценка , полученная по данным, имеющимся для моментов времени до k - i включительно, т. е. по y(k), у(k-1), ...., у(1), u(k-1), u(k-2), ..., u(1), определяется выражением

Оптимальное управление для задачи (8.9)-(8.11) имеет вид

и(k) = (k)× у(k),           

если известно значение q. Если же значение q неизвестно, то оно заменяется оценкой и управление принимает вид

Можно ожидать, что алгоритм управления (8.12)-(8.13) будет хорошо работать, если с = 0 и b= 1. В этом случае среднеквадратическая оценка q сходится к а приk®¥, а оценка управления сходится к u(k)=ay(k), т. е. в силу (8.10) - к оптимальному управлению.

Замечательное свойство алгоритма (8.12)—(8.13) состоит в том, что он сходится к оптимальному управлению (8.10) даже тогда, когда с¹ 0. Этот факт иллюстрируется на рис. 8.2, где показана оценка параметра q для а = - 0,9; b = 3 и с = - 0.3. Отметим, что оценка q сходится к  = -0,2, а не к значению а, равному –0,9. Значение  = -0,2 соответствует управлению, минимизирующему дисперсию ошибки.

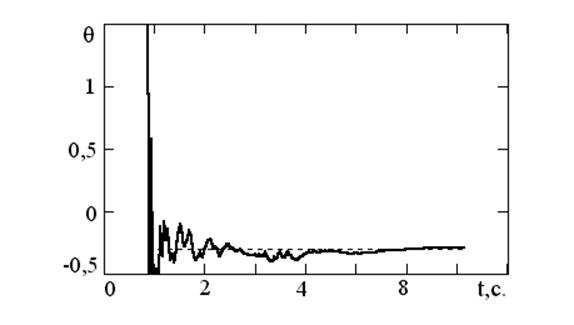
Рис. 8.2.

Для сравнения самонастраивающегося регулятора с оптимальным регулятором, полученным при известных точных значениях параметров, вычислим значение функционала

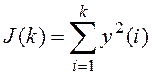
для самонастраивающегося регулятора и оптимального регулятора

u(k) = -0,2×y(k).

Рассмотренный пример показывает, что простой самонастраивающийся регулятор (8.12)-(8.13) обладает очень хорошими характеристиками. После короткого переходного периода он ведет себя практически так же, как и оптимальный регулятор с точными значениями параметров. При этом параметр q, судя по всему, сходится к значению, соответствующему регулятору, минимизирующему дисперсию ошибки.

Проведем эти эмпирические рассуждения на более формальном уровне. Предположим, что система описывается уравнением

где п - возмущение. Если возмущение ограничено в том смысле, что

то среднеквадратическое значение выхода замкнутой системы

также ограничено.

Это утверждение можно доказать рассуждением от противного. Если у не ограничено, то влиянием n(k) в (8.14) можно пренебречь. Тогда  будет сходиться     к а. Выбрав управление вида

u(k) = a×y(k),