Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 61

C =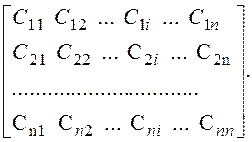

Уравнение (5.13) в развернутой форме имеет вид

…………………………………………………………

…………………………………………………………

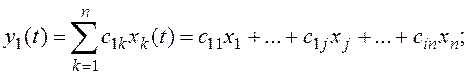
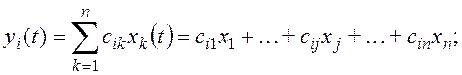
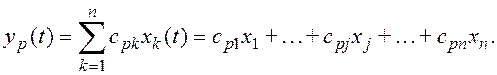
Из этих уравнений следует, что переменная x_j может быть определена по переменным y_1, y_{2, . . . ,} y_p, если коэффициенты  c_ij (для i = 1, 2, . . . , p) не все равны нулю. Другими словами, x_j является наблюдаемой переменной, если элементы j-го столбца матрицы С не все равны нулю, или линейная, стационарная система является наблюдаемой, если матрица выхода С не содержит столбцов, элементы которых равны нулю.

Условия наблюдаемости в общем случае определяются следующей теоремой (или критерием).

Необходимые и достаточные условия для полной наблюдаемости системы (5.13) состоят в том, чтобы матрица

имела ранг n.

Из выражения (5.16) очевидно, что наблюдаемость определяется свойствами матриц А и С. Так же как и в случае критерия управляемости, если матрица R имеет ранг n для некоторого m< n, т. е.

то наименьшее m, при котором имеет место равенство (5.16), называется показателем наблюдаемости.

Любая система, описываемая уравнениями состояния (5.13), может быть представлена в виде структурной схемы, изображенной на рисунке 5.9.

Значение понятий "управляемость" и "наблюдаемость". Возможно существование двух особых значений или мод (одной неуправляемой при  s = 1  и другой - ненаблюдаемой при s = -1). Для простой одномерной системы неуправляемость и ненаблюдаемость легко обнаружить непосредственно по ее уравнениям или структурной схеме (рис. 5.3).

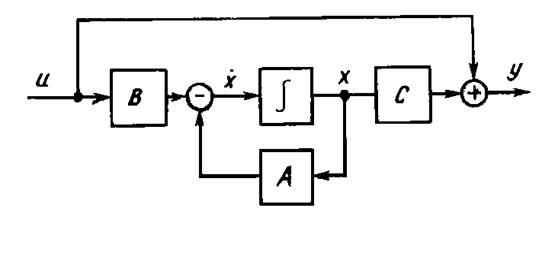
Рис. 5.9.

Рассмотрим теперь пример, когда система описывается передаточной функцией. Эта система, состоящая из двух последовательно соединенных подсистем с передаточными функциями

 ;   

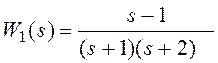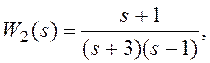
показана на рис. 5.10.

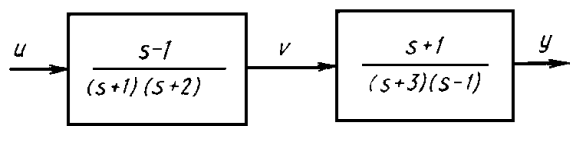
Рис. 5.10.

Передаточная функция системы

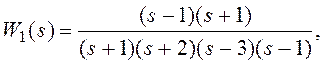
или

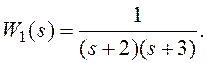
После сокращений нули и полюса при s = ± 1 выпали из рассмотрения. Однако такое сокращение полюса и нуля возможно лишь теоретически. На самом же деле такое сокращение не учитывает образование диполя (рис. 5.11). Если этот диполь расположен в левой полуплоскости вблизи точки -a, то ему в переходном процессе будет соответствовать член вида re^-at, где r - вычет, связанный с полюсом. Последний очень мал, так как вблизи полюса расположен нуль. В большинстве случаев этим членом можно пренебречь. Если же диполь расположен в правой полуплоскости, то он даст неустойчивый член re^at , каким бы малым r не было.

Заметим, что если по стрелке (от входа к выходу) сначала расположен нуль, а затем полюс, как, например при s = 1, то имеет место неуправляемость. А если по  стрелке  сначала  расположен  полюс, а  затем  нуль, как,  например при s = -1, то имеет место, ненаблюдаемость.

В случае многомерных систем с многими входами и выходами, когда сокращение может происходить в результате свойств определителей, обнаружение неуправляемости и ненаблюдаемости гораздо сложнее. Однако во всех случаях это происходит из-за тех или иных сокращений между подсистемами. Следует подчеркнуть различие между неуправляемыми (или ненаблюдаемыми) полюсами (или нулями) в зависимости от того, расположены они в левой или в правой полуплоскости.

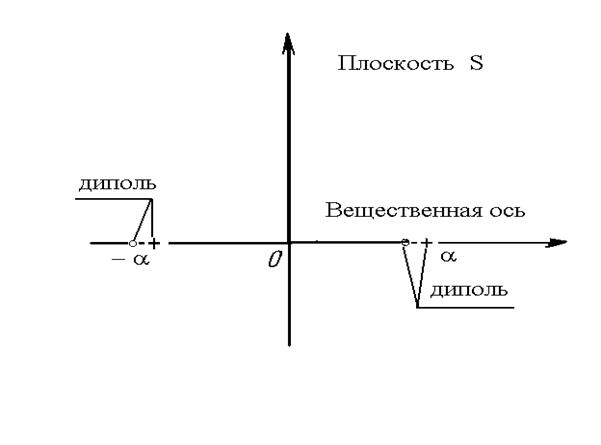
Рис. 5.11.

Предположим, что в системе имеется наблюдаемый, но не управляемый неустойчивый полюс. Так как он наблюдаем, то выход неустойчив. Он не может быть не замечен, но его неуправляемость исключает возможность управления системой. В этом случае выходом из положения может быть не изменение закона регулирования, а изменение структуры системы.

Предположим теперь, что система имеет управляемый, но не наблюдаемый неустойчивый полюс. Так как этот полюс не связан с выходом, то выход будет наблюдаться как устойчивый. Но тем не менее, внутренняя неустойчивость системы может привести к аварии, когда неустойчивая переменная достигнет определенной амплитуды, либо к появлению эффекта насыщения из-за выхода системы из линейной зоны.